



Next: Correlazione fra diverse combinazioni
Up: Valore atteso e varianza
Previous: Valore atteso e varianza
Indice
Una applicazione di particolare interesse
della proprietà della varianza è quella relativa alla
media aritmetica effettuata  variabili casuali analoghe,
aventi tutte la stessa distribuzione
e indipendenti l'una dall'altra (ad esempio l'
variabili casuali analoghe,
aventi tutte la stessa distribuzione
e indipendenti l'una dall'altra (ad esempio l'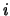 -mo
esito di un esperimento condotto in condizioni apparentemente identiche):
-mo
esito di un esperimento condotto in condizioni apparentemente identiche):
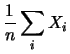 |
 |
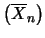 |
(10.41) |
E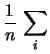 |
 |
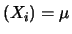 E E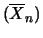 |
(10.42) |
Var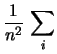 |
 |
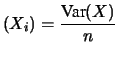 Var Var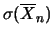 |
(10.43) |
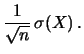 |
 |
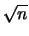 |
(10.44) |
La media aritmetica ha la stessa previsione della singola
variabile, ma un'incertezza 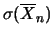 minore. Questo è un
risultato molto importante per quanto riguarda le misure
e sarà ripreso nel seguito. Detto alla buona, esso giustifica
l'idea intuitiva che il valore ottenuto da una media di
molte misure
è più affidabile di quello ottenuto da una singola
misura. L'espressione di
minore. Questo è un
risultato molto importante per quanto riguarda le misure
e sarà ripreso nel seguito. Detto alla buona, esso giustifica
l'idea intuitiva che il valore ottenuto da una media di
molte misure
è più affidabile di quello ottenuto da una singola
misura. L'espressione di
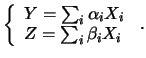 fornisce una espressione quantitativa dell'incremento della
``qualità'' della media aritmetica in funzione del numero di prove.
fornisce una espressione quantitativa dell'incremento della
``qualità'' della media aritmetica in funzione del numero di prove.




Next: Correlazione fra diverse combinazioni
Up: Valore atteso e varianza
Previous: Valore atteso e varianza
Indice
Giulio D'Agostini
2001-04-02
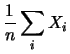
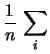
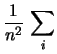
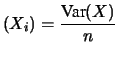 Var
Var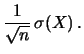
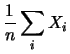
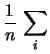
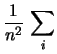
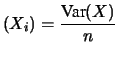 Var
Var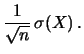
 fornisce una espressione quantitativa dell'incremento della
``qualità'' della media aritmetica in funzione del numero di prove.
fornisce una espressione quantitativa dell'incremento della
``qualità'' della media aritmetica in funzione del numero di prove.