



Next: Valore atteso e varianza
Up: Funzioni di variabili casuali
Previous: Riepilogo di alcune proprietà
Indice
Valore atteso e varianza di
combinazioni lineari
Sviluppiamo ora il programma illustrato all'inizio di questo capitolo
e schematizzato nella (10.3). Calcoliamo quindi
il valore atteso di una combinazione lineare di variabili casuali,
cominciando dal caso più semplice, quello della somma algebrica:
Nel caso generale
Avendo ottenuto il valore della previsione, interessiamoci
all'incertezza di previsione, data dalla deviazione standard.
Anche in questo caso cominciamo dalla somma algebrica:
Var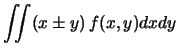 |
 |
E![$\displaystyle \left[\left((X\pm Y)-\mbox{E}(X\pm Y)\right)^2\right]$](img2800.png) |
|
| |
 |
E![$\displaystyle \left[\left(X-\mbox{E}(X)\right) \pm
\left(Y-\mbox{E}(Y)\right)^2\right]$](img2801.png) |
|
| |
 |
E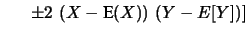 |
(10.26) |
| |
|
![$\displaystyle \ \ \ \ \ \ \left. \pm
2\, \left(X-\mbox{E}(X)\right)\, \left(Y-E[Y]\right)\right]
\nonumber$](img2803.png) |
|
| |
 |
Var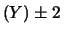 Var Var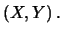 Cov Cov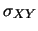 |
(10.27) |
Nel caso in cui la covarianza si annulla
troviamo
che la varianza di una somma o differenza di due variabili casuali
è uguale alla somma delle varianze.
Utilizando i simboli compatti di 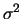 per la varianza
e
per la varianza
e
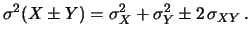 per la covarianza, possiamo riscrivere
la 10.27 come
per la covarianza, possiamo riscrivere
la 10.27 come
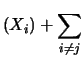 |
(10.28) |
Nel caso di una somma di  variabili
variabili
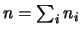 otteniamo:
otteniamo:
E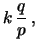 |
 |
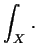 E E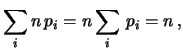 |
(10.29) |
Var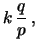 |
 |
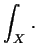 Var Var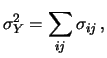 Cov Cov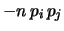 |
(10.30) |
e, nella notazione simmetrica appena introdotta:
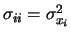 |
(10.31) |
ove
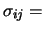 e
e
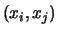 Cov
Cov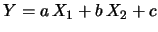 .
Consideriamo infine una combinazione lineare di due variabili
.
Consideriamo infine una combinazione lineare di due variabili
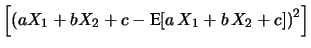 :
:
Var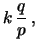 |
 |
E![$\displaystyle \left[\left(aX_1+bX_2+c-\mbox{E}[a\, X_1+b\, X_2+c]
\right)^2\right]$](img2815.png) |
|
| |
 |
E![$\displaystyle \left[\left(a\, (X_1-\mbox{E}(X_1))+b\,
(X_2-\mbox{E}(X_2))\right)^2\right]$](img2816.png) |
|
| |
 |
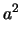 Var Var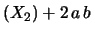 Var Var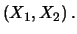 Cov Cov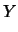 |
|
| |
|
|
(10.32) |
Questo risultato può essere esteso a un numero qualsiasi di
variabili:
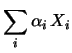 |
 |
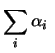 |
|
E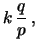 |
 |
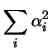 E E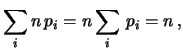 |
(10.33) |
| Var(Y) |
 |
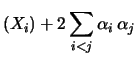 Var Var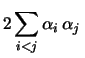 Cov Cov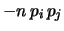 |
(10.34) |
Possiamo riscrivere in modo più compatto
l'espressione della covarianza, osservando innanzitutto che
in quanto il fattore 2 è dovuto a considerare sia 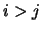 che
che 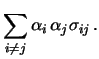 .
Utilizzando inoltre la notazione compatta, questa può essere riscritta
come
Anche i termini dovuti alle varianze possono
essere riscritti come
.
Utilizzando inoltre la notazione compatta, questa può essere riscritta
come
Anche i termini dovuti alle varianze possono
essere riscritti come
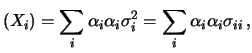
Var
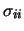
ove
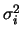 sta per
sta per
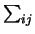 .
Per concludere, il modo più compatto di scrivere la varianza di una
combinazione lineare10.8è:
.
Per concludere, il modo più compatto di scrivere la varianza di una
combinazione lineare10.8è:
Vediamo due applicazioni di quanto abbiamo mostrato in questo paragrafo.
Subsections




Next: Valore atteso e varianza
Up: Funzioni di variabili casuali
Previous: Riepilogo di alcune proprietà
Indice
Giulio D'Agostini
2001-04-02
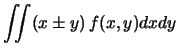
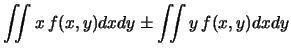
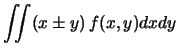
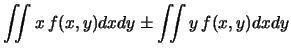
![]() per la varianza
e
per la varianza
e
![]() per la covarianza, possiamo riscrivere
la 10.27 come
per la covarianza, possiamo riscrivere
la 10.27 come
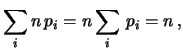
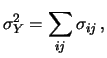 Cov
Cov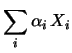
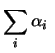
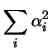 E
E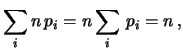
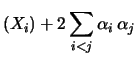 Var
Var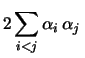 Cov
Cov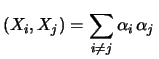 Cov
Cov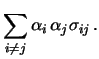 .
Utilizzando inoltre la notazione compatta, questa può essere riscritta
come
.
Utilizzando inoltre la notazione compatta, questa può essere riscritta
come
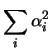
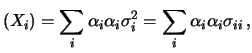 Var
Var