



Next: Soluzione generale per variabili
Up: Funzioni di variabili casuali
Previous: Funzioni di variabili casuali
Indice
La condizione di incertezza su alcune grandezze si riflette
in genere su ogni altra grandezza che sia funzione di esse.
Ad esempio,
immaginiamo di essere
interessati all'area ( ) e al perimetro (
) e al perimetro ( ) di un rettangolo
(idealizzazione del piano di un tavolo), di cui sono stati
misurati i due lati (
) di un rettangolo
(idealizzazione del piano di un tavolo), di cui sono stati
misurati i due lati ( e
e 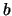 ).
L'inevitabile incertezza sul valore di
).
L'inevitabile incertezza sul valore di  e di
e di 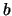 (a cui andrebbe aggiunta quella legata al fatto che il
quadrilatero potrebbe essere non perfettamente retto)
si riflette su
(a cui andrebbe aggiunta quella legata al fatto che il
quadrilatero potrebbe essere non perfettamente retto)
si riflette su  e su
e su  . Il termine con cui questo processo
è noto è propagazione delle incertezze.
. Il termine con cui questo processo
è noto è propagazione delle incertezze.
Come sappiamo, i gradi di fiducia sui possibili valori di  e di
e di
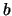 sono espressi da
sono espressi da 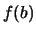 e
e 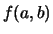 . Ma, nel caso generale,
i valori10.1di
. Ma, nel caso generale,
i valori10.1di  e di
e di 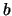 non sono indipendenti, come può
succedere nel caso che i lati siano stati misurati con lo stesso strumento,
non perfettamente calibrato10.2. Quindi, in genere bisognerà considerare la
funzione congiunta
non sono indipendenti, come può
succedere nel caso che i lati siano stati misurati con lo stesso strumento,
non perfettamente calibrato10.2. Quindi, in genere bisognerà considerare la
funzione congiunta 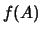 .
Per poter quantificare nel modo più generale
l'incertezza su area e perimetro,
bisogna imparare a valutare
.
Per poter quantificare nel modo più generale
l'incertezza su area e perimetro,
bisogna imparare a valutare 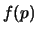 e
e 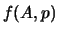 partendo da
partendo da 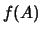 (o da
(o da 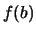 e
e 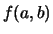 nel caso di indipendenza). In realtà, anche
in questo caso, la soluzione più generale al problema
si ottiene mediante il calcolo di
nel caso di indipendenza). In realtà, anche
in questo caso, la soluzione più generale al problema
si ottiene mediante il calcolo di 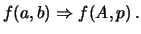 . Infatti ci aspettiamo
che
. Infatti ci aspettiamo
che  e
e  abbiano un certo grado di correlazione, in quanto
sono calcolate dalle stesse informazioni di partenza.
Riepilogando, il problema consiste nel valutare
abbiano un certo grado di correlazione, in quanto
sono calcolate dalle stesse informazioni di partenza.
Riepilogando, il problema consiste nel valutare 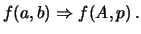 a partire da
a partire da 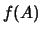 :
:
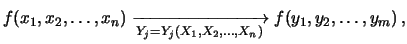 |
(10.1) |
Come vedremo, il problema generale può diventare abbastanza complesso
dal punto di vista del calcolo. Ci accontenteremo di calcolare
soltanto previsione e incertezza di previsione
delle varie grandezze e, qualora esistano correlazioni,
del loro coefficiente di correlazione. Nella maggior parte dei
casi pratici (e ``tranquilli'') queste approssimazioni sono
più che ragionevole e vedremo come esse ci permetteranno,
sotto certe ipotesi spesso soddisfatte, di effettuare
affermazioni probabilistiche sui valori delle grandezza.
È comunque importante ricordarsi che, all'occorrenza,
bisogna affrontare il problema nel modo più
rigoroso, descritto da una generalizzazione della
(10.1), che scriviamo con
![$\displaystyle f(x_1, x_2,\ldots, x_n)\xrightarrow[Y_j = Y_j(X_1, X_2,\ldots, X_n)]{}f(y_1, y_2,\ldots, y_m)\,,$](img2598.png) |
(10.2) |
ove con
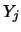 è indicata la
è indicata la 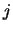 -ma funzione
che lega le
-ma funzione
che lega le 
 alle
alle 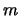
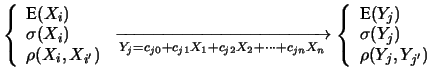 .
La soluzione minimale che affronteremo nei dettagli
sarà invece il solo caso di propagazione
di previsione ed incertezza di combinazioni lineari di variabili:
.
La soluzione minimale che affronteremo nei dettagli
sarà invece il solo caso di propagazione
di previsione ed incertezza di combinazioni lineari di variabili:
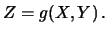 |
(10.3) |
A questo caso ci ridurremo, previe linearizazioni,
nel caso di funzioni qualsiasi (e nei limiti in cui le
linearizzazioni siano ragionevoli).
I prossimi paragrafi, dedicati alla valutazione della distribuzione
di probabilità di funzioni di variabili casuali, possono essere
saltati da chi non è interessato a tale argomento. In tale caso si
vada direttamente al paragrafo 10.6.




Next: Soluzione generale per variabili
Up: Funzioni di variabili casuali
Previous: Funzioni di variabili casuali
Indice
Giulio D'Agostini
2001-04-02
![]() e di
e di
![]() sono espressi da
sono espressi da ![]() e
e ![]() . Ma, nel caso generale,
i valori10.1di
. Ma, nel caso generale,
i valori10.1di ![]() e di
e di ![]() non sono indipendenti, come può
succedere nel caso che i lati siano stati misurati con lo stesso strumento,
non perfettamente calibrato10.2. Quindi, in genere bisognerà considerare la
funzione congiunta
non sono indipendenti, come può
succedere nel caso che i lati siano stati misurati con lo stesso strumento,
non perfettamente calibrato10.2. Quindi, in genere bisognerà considerare la
funzione congiunta ![]() .
Per poter quantificare nel modo più generale
l'incertezza su area e perimetro,
bisogna imparare a valutare
.
Per poter quantificare nel modo più generale
l'incertezza su area e perimetro,
bisogna imparare a valutare ![]() e
e ![]() partendo da
partendo da ![]() (o da
(o da ![]() e
e ![]() nel caso di indipendenza). In realtà, anche
in questo caso, la soluzione più generale al problema
si ottiene mediante il calcolo di
nel caso di indipendenza). In realtà, anche
in questo caso, la soluzione più generale al problema
si ottiene mediante il calcolo di ![]() . Infatti ci aspettiamo
che
. Infatti ci aspettiamo
che ![]() e
e ![]() abbiano un certo grado di correlazione, in quanto
sono calcolate dalle stesse informazioni di partenza.
Riepilogando, il problema consiste nel valutare
abbiano un certo grado di correlazione, in quanto
sono calcolate dalle stesse informazioni di partenza.
Riepilogando, il problema consiste nel valutare ![]() a partire da
a partire da ![]() :
:
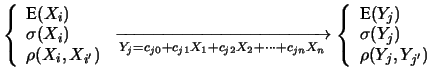 .
La soluzione minimale che affronteremo nei dettagli
sarà invece il solo caso di propagazione
di previsione ed incertezza di combinazioni lineari di variabili:
.
La soluzione minimale che affronteremo nei dettagli
sarà invece il solo caso di propagazione
di previsione ed incertezza di combinazioni lineari di variabili: