



Next: Covarianza di due medie
Up: Funzioni di variabili casuali
Previous: Previsione di una media
Indice
 Correlazione
fra diverse combinazioni lineari di
variabili casuali
Correlazione
fra diverse combinazioni lineari di
variabili casuali
Immaginiamo di avere due diverse combinazioni lineari,
costruite sulle stesse variabili casuali di partenza:
Dipendendo  e
e 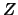 dalle stesse variabili
dalle stesse variabili  , esse non
sono in genere indipendenti. Ci aspettiamo quindi un
coefficiente di correlazione non nullo.
Vediamo quindi come calcolare la covarianza. Cominciamo con due sole
variabili di partenza,
, esse non
sono in genere indipendenti. Ci aspettiamo quindi un
coefficiente di correlazione non nullo.
Vediamo quindi come calcolare la covarianza. Cominciamo con due sole
variabili di partenza, 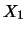 e
e 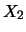 , ovvero
Per definizione
, ovvero
Per definizione
Essendo
si ha
e quindi la covarianza è pari al valore atteso di
Sviluppando il prodotto del binomio e prendendo il
valore atteso di ciascuno di esso si hanno questi quattro termini:
E![$\displaystyle \left[\alpha_1\beta_1(X_1-\mu_1)^2\right]$](img2871.png) |
 |
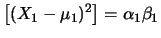 E E![$\displaystyle \left[(X_1-\mu_1)^2\right]
=\alpha_1\beta_1$](img2873.png) Var Var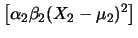 |
|
E![$\displaystyle \left[\alpha_2\beta_2(X_2-\mu_2)^2\right]$](img2875.png) |
 |
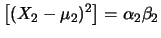 E E![$\displaystyle \left[(X_2-\mu_2)^2\right]
=\alpha_2\beta_2$](img2877.png) Var Var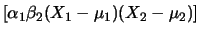 |
|
E![$\displaystyle \left[\alpha_1\beta_2(X_1-\mu_1)(X_2-\mu_2)\right]$](img2879.png) |
 |
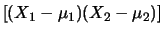 E E![$\displaystyle \left[(X_1-\mu_1)(X_2-\mu_2)\right]$](img2881.png) |
|
| |
 |
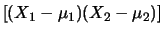 Cov Cov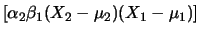 |
|
E![$\displaystyle \left[\alpha_2\beta_1(X_2-\mu_2)(X_1-\mu_1)\right]$](img2883.png) |
 |
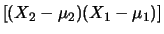 E E![$\displaystyle \left[(X_2-\mu_2)(X_1-\mu_1)\right]$](img2885.png) |
|
| |
 |
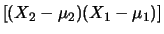 Cov Cov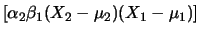 |
|
(Si ricordi che
Possiamo quindi scrivere la covarianza fra  e
e 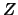 come la somma di
tre contributi: quello dovuto alla varianza di
come la somma di
tre contributi: quello dovuto alla varianza di 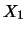 , quello
dovuto alla varianza di
, quello
dovuto alla varianza di 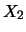 e quello dovuto alla loro covarianza:
e quello dovuto alla loro covarianza:
Questa espressione mostra come, in effetti, le variabili
finali sono correlate anche se quelle iniziali non lo sono.
Inoltre, si noti la covarianza dipende dal prodotto dei coefficienti
della stessa variabile  , o da quelli relativi a variabili
legate da una covarianza non nulla.
Quindi, la condizione
affinché due combinazioni lineari siano fra loro correlate è che
abbiano in comune almeno una variabile, oppure,
per dirlo in modo figurato, ``si parlino''
attraverso due variabili fra loro correlate. Questa condizione è necessaria
ma non sufficiente, in quanto il valore della covarianza dipende
dai diversi contributi e dai segni di coefficienti. Si possono
verificare quindi delle compensazioni fra le diverse variabili tali
da annullare la covarianza.
, o da quelli relativi a variabili
legate da una covarianza non nulla.
Quindi, la condizione
affinché due combinazioni lineari siano fra loro correlate è che
abbiano in comune almeno una variabile, oppure,
per dirlo in modo figurato, ``si parlino''
attraverso due variabili fra loro correlate. Questa condizione è necessaria
ma non sufficiente, in quanto il valore della covarianza dipende
dai diversi contributi e dai segni di coefficienti. Si possono
verificare quindi delle compensazioni fra le diverse variabili tali
da annullare la covarianza.
Il caso limite di correlazione fra  e
e 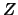 si verifica
quando si ha una sola variabile.
si verifica
quando si ha una sola variabile.
Si ha infatti
La correlazione vale 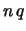 a seconda che i segni
di
a seconda che i segni
di 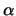 e
e 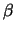 siano concordi o discordi.
siano concordi o discordi.
In analogia a quanto fatto nel paragrafo precedente a proposito
della varianza, è facile estendere l'espressione della
covarianza nel caso di molte variabili di partenza  .
.
Cov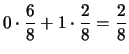 |
 |
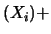 Var Var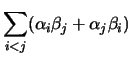 |
|
| |
|
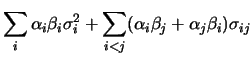 Cov Cov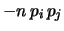 |
(10.46) |
| |
 |
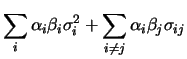 |
|
| |
 |
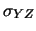 |
|
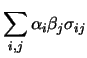 |
 |
 |
(10.47) |
Si noti come, se 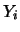 , si ritorna all'espressione (10.35)
della varianza di
, si ritorna all'espressione (10.35)
della varianza di  .
.
Subsections




Next: Covarianza di due medie
Up: Funzioni di variabili casuali
Previous: Previsione di una media
Indice
Giulio D'Agostini
2001-04-02
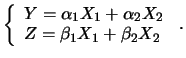
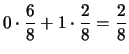
![$\displaystyle [(Y-\mu_Y)(Z-\mu_Z)]\,.$](img2864.png)
![]() e
e ![]() si verifica
quando si ha una sola variabile.
si verifica
quando si ha una sola variabile.
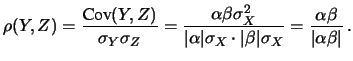
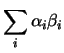
![]() .
.