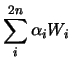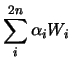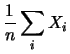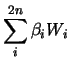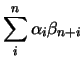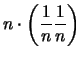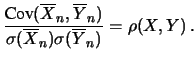Next: Correlazione fra una variabile
Up: Correlazione fra diverse combinazioni
Previous: Correlazione fra diverse combinazioni
Indice
Immaginiamo di ripetere molte volte un
esperimento, sotto condizioni apparentemente identiche,
e che per l' -mo esperimento si misurino due grandezze
-mo esperimento si misurino due grandezze
 e
e 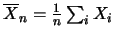 . I possibili esiti degli esperimenti
saranno
. I possibili esiti degli esperimenti
saranno  coppie di variabili casuali analoghe,
cioè tutte aventi la stessa distribuzione di probabilità.
Nel caso generale
coppie di variabili casuali analoghe,
cioè tutte aventi la stessa distribuzione di probabilità.
Nel caso generale  e
e 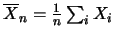 non sono in genere indipendenti e
avremo quindi una covarianza
Cov
non sono in genere indipendenti e
avremo quindi una covarianza
Cov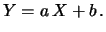 (è stato omesso
l'indice
(è stato omesso
l'indice 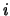 in quanto la covarianza è la stessa per tutte
le coppie. Applichiamo ora i risultati del paragrafo precedente per
calcolare la covarianza fra le due medie aritmetiche
in quanto la covarianza è la stessa per tutte
le coppie. Applichiamo ora i risultati del paragrafo precedente per
calcolare la covarianza fra le due medie aritmetiche
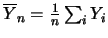 e
e
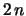 .
Al fine di utilizzare le formule precedenti si consideri
.
Al fine di utilizzare le formule precedenti si consideri
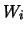 variabili
variabili 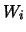 , tali che
, tali che
Le due medie possono essere riscritte come
I coefficienti 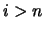 valgono
valgono 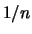 per
per 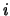 compreso fra 1 e
compreso fra 1 e  ,
mentre sono nulli per
,
mentre sono nulli per 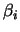 . Viceversa
. Viceversa 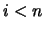 sono nulli
per
sono nulli
per 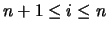 e valgono
e valgono 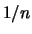 per
per
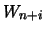 .
Osservando la (10.46) (riscritta
in termini delle
.
Osservando la (10.46) (riscritta
in termini delle 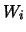 ), notiamo che i soli contributi
non nulli sono quelli dovuti alla covarianza fra
), notiamo che i soli contributi
non nulli sono quelli dovuti alla covarianza fra 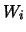 e
e
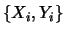 , corrispondenti alla coppia
, corrispondenti alla coppia
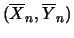 10.9.
Ne segue che
10.9.
Ne segue che
Come la varianza, anche la covarianza delle medie è 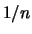 volte inferiore alla covarianza di ciascuna coppia di variabili.
Rimane invece invariato il coefficiente di correlazione:
volte inferiore alla covarianza di ciascuna coppia di variabili.
Rimane invece invariato il coefficiente di correlazione:




Next: Correlazione fra una variabile
Up: Correlazione fra diverse combinazioni
Previous: Correlazione fra diverse combinazioni
Indice
Giulio D'Agostini
2001-04-02