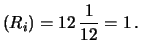Next: Linearizzazione
Up: Funzioni di variabili casuali
Previous: Estensione del teorema del
Indice
pzd100 Simulazione di numeri aleatori distribuiti
secondo una distribuzione normale
Abbiamo visto nel paragrafo 8.3 alcune tecniche
per simulare numeri aleatori. Vediamone un'altra, di semplice
implementazione che permette di generare dei numeri
secondo una distribuzione normale.
Consideriamo, come al solito in questi casi, la variabile 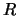 distribuita
uniformemente fra 0 e 1. Consideriamo 12 variabili indipendenti
distribuita
uniformemente fra 0 e 1. Consideriamo 12 variabili indipendenti 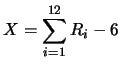 e costruiamo la nuova variabile casuale
e costruiamo la nuova variabile casuale
di valore atteso e varianza pari a
E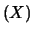 |
 |
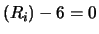 E E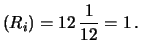 |
(10.59) |
Var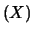 |
 |
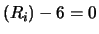 Var Var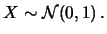 |
(10.60) |
Quindi, poiché come abbiamo visto,
a partire da distribuzioni uniformi simili la convergenza
è molto rapida, per il teorema del limite centrale
Per ottenere qualsiasi altra distribuzione normale  di parametri
di parametri  e
e  è sufficiente effettuare la trasformazione
Un esempio di istogramma ottenuto con questo metodo è mostrato
in figura 10.4 per
è sufficiente effettuare la trasformazione
Un esempio di istogramma ottenuto con questo metodo è mostrato
in figura 10.4 per 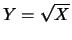 e
e 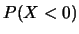 .
.
Si noti come, ovviamente, la tecnica non riproduce bene il
comportamento delle code estreme, ma la si può migliorare
aumentando il numero di termini della somma (e modificando opportunamente
le formule).




Next: Linearizzazione
Up: Funzioni di variabili casuali
Previous: Estensione del teorema del
Indice
Giulio D'Agostini
2001-04-02
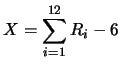 e costruiamo la nuova variabile casuale
e costruiamo la nuova variabile casuale
![]() distribuita
uniformemente fra 0 e 1. Consideriamo 12 variabili indipendenti
distribuita
uniformemente fra 0 e 1. Consideriamo 12 variabili indipendenti 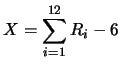 e costruiamo la nuova variabile casuale
e costruiamo la nuova variabile casuale