



Next: Riepilogo di alcune proprietà
Up: Funzioni di variabili casuali
Previous: , con e gaussiane
Indice
pzd100 Stime a bruta forza:
metodi di Monte Carlo
Un metodo pratico molto usato per stimare le
distribuzioni di probabilità di funzioni complicate
di variabili casuali consiste nell'utilizzare delle
tecniche di simulazione al computer. Tenendo conto che in pratica
anche le funzioni continue sono discretizzate per eseguire i calcoli,
non si fa altro che applicare che applicare la regola generale
incontrata nel paragrafo 10.2.1
(formula (10.6), (10.5), o loro
generalizzazione a molte dimensioni).
Il caso più semplice consiste nello stimare
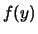 a partire da
a partire da
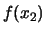 ,
, 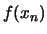 ,...
,...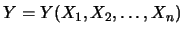 ,
sapendo che
,
sapendo che
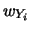 e assumendo che le
variabili di partenza
e assumendo che le
variabili di partenza  siano fra loro indipendenti. I passi richiesti
sono i seguenti:
siano fra loro indipendenti. I passi richiesti
sono i seguenti:
- estrarre le variabili
 usando, ad esempio, una delle tecniche
descritte nel paragrafo 8.3;
usando, ad esempio, una delle tecniche
descritte nel paragrafo 8.3;
- valutare la funzione
 in corrispondenza dei valori
in corrispondenza dei valori  ;
;
- istogrammare la variabile
 e ripetere il processo
un numero di volte
e ripetere il processo
un numero di volte  .
.
Si calcola infine la frequenza relativa 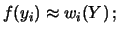 con cui
il valore
con cui
il valore  compare nelle diverse classi dell'istogramma.
Poiché al crescere di
compare nelle diverse classi dell'istogramma.
Poiché al crescere di  si è sempre più sicuri che
la distribuzione statistica delle frequenze che si otterrà
sarà molto vicina alla distribuzione di probabilità
(vedi paragrafi 7.13 e
7.14, nonché prossimo paragrafo
10.9.2) la distribuzione di probabilità è
stimata nel seguente modo:
si è sempre più sicuri che
la distribuzione statistica delle frequenze che si otterrà
sarà molto vicina alla distribuzione di probabilità
(vedi paragrafi 7.13 e
7.14, nonché prossimo paragrafo
10.9.2) la distribuzione di probabilità è
stimata nel seguente modo:
- A) caso discreto
- B) caso continuo
ove 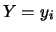 indica la frequenza relativa di occorrenze del valore
indica la frequenza relativa di occorrenze del valore
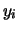 (caso discreto) o delle volte in cui il valore
della
(caso discreto) o delle volte in cui il valore
della  è risultato compreso fra
è risultato compreso fra 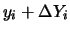 e
e
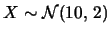 (caso continuo). Un esempio di applicazione
verrà mostrato in figura 10.5 a proposito del
teorema del limite centrale.
L'estensione al caso di più variabili di arrivo
(caso continuo). Un esempio di applicazione
verrà mostrato in figura 10.5 a proposito del
teorema del limite centrale.
L'estensione al caso di più variabili di arrivo 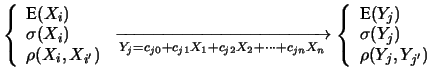 o a quello in cui le variabile di partenza sono correlate
è semplice dal punto di vista concettuale,
anche se l'implementazione al computer può essere non
proprio banale.
o a quello in cui le variabile di partenza sono correlate
è semplice dal punto di vista concettuale,
anche se l'implementazione al computer può essere non
proprio banale.
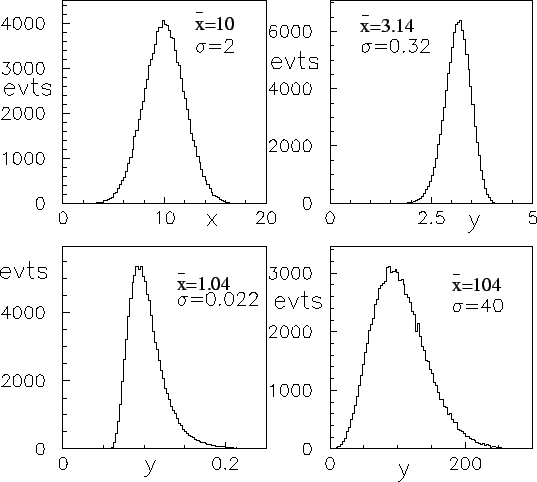
Figura:
Esempi di trasformazione di una variabile normale:
 ;
; 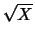 ;
; 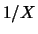 ;
; 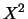 .
.
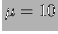 |
Un esempio di questa tecnica è mostrato in figura 10.4,
ove una variabile casuale  distribuita secondo una distribuzione
normale di
distribuita secondo una distribuzione
normale di 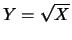 e
e 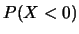 è generata
è generata
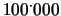 volte
con la tecnica di
Monte Carlo (vedi paragrafo 10.12) e successivamente
trasformata in
volte
con la tecnica di
Monte Carlo (vedi paragrafo 10.12) e successivamente
trasformata in
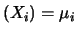 ,
, 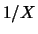 e
e 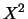 (nell'ordine e come
facilmente riconoscibile dai valori medi e deviazioni
standard delle distribuzioni statistiche risultanti dalla simulazione).
(nell'ordine e come
facilmente riconoscibile dai valori medi e deviazioni
standard delle distribuzioni statistiche risultanti dalla simulazione).




Next: Riepilogo di alcune proprietà
Up: Funzioni di variabili casuali
Previous: , con e gaussiane
Indice
Giulio D'Agostini
2001-04-02
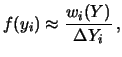
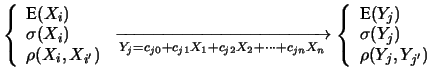 o a quello in cui le variabile di partenza sono correlate
è semplice dal punto di vista concettuale,
anche se l'implementazione al computer può essere non
proprio banale.
o a quello in cui le variabile di partenza sono correlate
è semplice dal punto di vista concettuale,
anche se l'implementazione al computer può essere non
proprio banale.