



Next: pzd100Convoluzione di due funzioni
Up: Soluzione generale per variabili
Previous: Soluzione generale per variabili
Indice
Regola generale
Consideriamo due variabili casuali di partenza,  e
e  ,
e soltanto una variabile,
,
e soltanto una variabile,
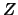 , funzione di esse:
Cominciamo dal considerare il caso in cui
, funzione di esse:
Cominciamo dal considerare il caso in cui 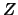 assuma
un certo valore
assuma
un certo valore 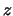 per la sola combinazione della variabili
per la sola combinazione della variabili
 e
e 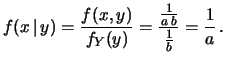 . Chiaramente, la probabilità di
. Chiaramente, la probabilità di 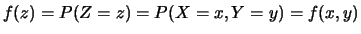 sarà uguale alla
probabilità che si verifichino esattamente questi valori di
sarà uguale alla
probabilità che si verifichino esattamente questi valori di  e di
e di  :
:
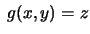 con con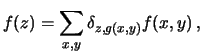 |
(10.4) |
Quando ci sono invece più coppie che contribuiscono al
valore 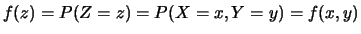 , bisogna
sommare su tutte le loro probabilità:10.3
, bisogna
sommare su tutte le loro probabilità:10.3
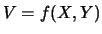 |
(10.5) |
Come esempio, si veda la somma degli esiti nel lancio
di due dadi,
già mostrato nel paragrafo 6.4
(vedi anche figura 6.2). Si noti come
l'alta probabilità per valori centrali della somma
sia dovuto soltanto al fatto che questi valori possono
essere causati da più combinazioni di quelli estremi.
La (10.5) si estende facilmente al caso di
più funzioni. Ad esempi, considerando anche la variabile
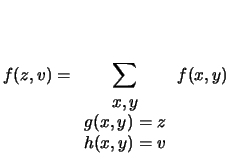 , la congiunta è data da:
, la congiunta è data da:
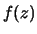 |
(10.6) |
Anche se l'impostazione della (10.6) è semplice,
il calcolo che permette di ottenere delle formule analitiche
può essere molto complicato, ben al di là dello scopo di questo corso.
Vediamo soltanto nei prossimi paragrafi alcuni sottocasi molto istruttivi.




Next: pzd100Convoluzione di due funzioni
Up: Soluzione generale per variabili
Previous: Soluzione generale per variabili
Indice
Giulio D'Agostini
2001-04-02
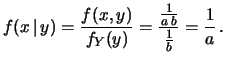 . Chiaramente, la probabilità di
. Chiaramente, la probabilità di 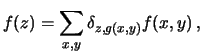
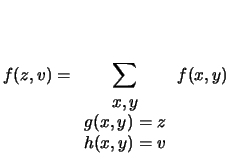 , la congiunta è data da:
, la congiunta è data da: