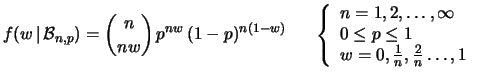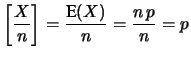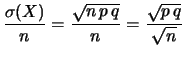Next: Previsione di una distribuzione
Up: Distribuzioni di probabilità di
Previous: pzd100Previsione, penalizzazione e valore
Indice
 Previsione di frequenza
relativa e legge dei grandi numeri
Previsione di frequenza
relativa e legge dei grandi numeri
Consideriamo la distribuzione binomiale degli  successi su
successi su
 prove. Dividendo il numero di successi per il numero
di prove otteniamo una nuova variabile casuale
associata alla frequenza relativa di successi.
La distribuzione di
prove. Dividendo il numero di successi per il numero
di prove otteniamo una nuova variabile casuale
associata alla frequenza relativa di successi.
La distribuzione di 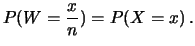 può essere ricavata direttamente
dalla binomiale in quanto
L'espressione della distribuzione di probabilità di
può essere ricavata direttamente
dalla binomiale in quanto
L'espressione della distribuzione di probabilità di 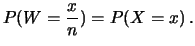 si ottiene
direttamente da quella di
si ottiene
direttamente da quella di  :
:
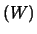 |
(7.32) |
Per il valore atteso e la sua incertezza abbiamo:
La previsione della frequenza relativa è pari alla probabilità
di ciascuno dei processi elementati di Bernoulli.
Inoltre l'incertezza di previsione decresce come
 , ovvero
al crescere di
, ovvero
al crescere di  diventa sempre meno probabile trovare
valori di frequenza che differiscono molto dalla probabilità.
Questo è uno dei modi di esprimere la legge dei grandi
numeri, sulla quale ritorneremo con maggiore
dettaglio nel capitolo 10.
diventa sempre meno probabile trovare
valori di frequenza che differiscono molto dalla probabilità.
Questo è uno dei modi di esprimere la legge dei grandi
numeri, sulla quale ritorneremo con maggiore
dettaglio nel capitolo 10.
Per ora utilizzeremo la variabile casuale frequenza relativa
per parlare delle previsioni di distribuzioni statistiche
e per introdurre la problematica della verifica delle
leggi statistiche.




Next: Previsione di una distribuzione
Up: Distribuzioni di probabilità di
Previous: pzd100Previsione, penalizzazione e valore
Indice
Giulio D'Agostini
2001-04-02