pzd100Previsione, penalizzazione e valore sul quale scommettere

Abbiamo parlato per esteso del valore atteso come media della distribuzione e abbiamo accennato alla moda e alla mediana, possibili alternative per quantificare sinteticamente la ditribuzione, definite rispettivamente come il valore di massima probabilità e quello centrale (nel senso di 50di probabilità a sinistra e 50% a destra).

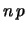Nel capitolo precedente abbiamo discusso dei diversi vantaggi della media. Anche parlando della distribuzione binomiale, abbiamo visto come la media dipenda linearmente da $p$ e riproduca il valore intuitivo $n\, p$ per il valore atteso. La tabella 7.5 mostra come cambiano i valori di media, moda e mediana al variare di $p$, avendo fissato $n$.

Tabella: Confronto fra media, moda e mediana per una distribuzione binomiale avente $n=10$ e per diversi valori di $p$.

$p$	media	moda	mediana
0.16	1.6	1	1
0.18	1.8	1	2
0.20	2.0	2	2
0.22	2.2	2	2
0.24	2.4	2	2
0.26	2.6	2	3
0.28	2.8	3	3

C'è un altro aspetto interessante di queste tre grandezze legato al valore sul quale scommettere, relativamente alle condizioni di vincita, o meglio alle condizioni di penalizzazione (vedi paragrafo 2.17). Infatti, è possibile che: *** chiarire ***

• nel caso si vinca soltanto se si verifica esattamente il valore sul quale si è scommesso conviene puntare sul valore più probabile, ovvero sulla moda;
• se vince chi scommette sul valore che più vicino a quello che si verifica conviene puntare sul valore centrale in probabilità, ovvero sulla mediana (analogalmente se si paga una penale che dipende dal modulo dello scarto) ** chiarire **
• se la penale va invece come il quadrato dello scarto, o vince realizza il minor quadrato dello scarto, conviene puntare sula media.

*** parlare anche dei vantaggi di moda e mediana nei casi in cui la media non esiste. ***