



Next: Lancio di una moneta
Up: Legge dei grandi numeri
Previous: Limite della media aritmetica
Indice
Teorema di Bernoulli
Riprendiamo quanto detto nel paragrafo
7.13. Considerando  prove indipendenti,
la previsione dellla frequenza relativa di successo,
che per comodità chiamiamo
prove indipendenti,
la previsione dellla frequenza relativa di successo,
che per comodità chiamiamo 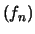 (uguale a
(uguale a 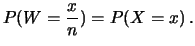 del paragrafo
7.13), abbiamo
del paragrafo
7.13), abbiamo
Procedendo per analogia al caso precedente otteniamo:
L'interpretazione di questa disuguaglianza, nota come
teorema di Bernoulli, è analoga
a quanto visto per
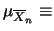 :
:
al crescere di  diventa sempre meno probabile
osservare valori di frequenze relative che differiscono molto da
diventa sempre meno probabile
osservare valori di frequenze relative che differiscono molto da  .
.
Essendo questo uno dei teoremi più intriganti del calcolo
delle probabilità, merita una serie di osservazioni.
- La formulazione va intesa in termini di probabilità e non di certezza.
- Il teorema non implica assolutamente che, se per un certo
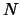 lo scarto
lo scarto 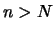 è grande, allora per
è grande, allora per  la frequanza relativa
la frequanza relativa 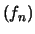 ``debba recuperare'' per ``mettersi in regola con la legge''.
(Nel seguito mostreremo, come esercizio, la fallacia dell'interpretazione
della legge dei grandi numeri per aspettarsi che i numeri ritardatari
al lotto recuperino.)
``debba recuperare'' per ``mettersi in regola con la legge''.
(Nel seguito mostreremo, come esercizio, la fallacia dell'interpretazione
della legge dei grandi numeri per aspettarsi che i numeri ritardatari
al lotto recuperino.)
- Esso non giustifica la ``definizione'' frequentista di probabilità.
Affermando infatti che ``è molto probabile che la frequenza non differisca
molto dalla probabilità'' si sta assumendo il concetto di probabilità.
Inoltre:
- Non si dimentichi che il teorema di Bernoulli ...è un teorema,
basato sulle regole di base dalla probabilità e su tutte le proprietà
che ne derivano. Quindi non può definire il concetto di probabilità.
- Su tale argomento è molto convincente de Finetti
``Per quanti tendono a ricollegare il concetto stesso
di probabilità alla nozione di frequenza, tali risultati
[che 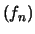 ``tenda a
``tenda a  ''] vengono ad assumere un ruolo di
cerniera per convalidare tale avvicinamento o identificazione
di nozioni. Logicamente non si sfugge però al dilemma che la
stessa cosa non si può assumere prima per definizione e poi
dimostrare come teorema, né alla contraddizione di una
definizione che assumerebbe una cosa certa mentre il teorema
afferma che è soltanto molto probabile.
''] vengono ad assumere un ruolo di
cerniera per convalidare tale avvicinamento o identificazione
di nozioni. Logicamente non si sfugge però al dilemma che la
stessa cosa non si può assumere prima per definizione e poi
dimostrare come teorema, né alla contraddizione di una
definizione che assumerebbe una cosa certa mentre il teorema
afferma che è soltanto molto probabile.
- Si noti inoltre che la condizione di
 costante implica
che essa sia prefissata a priori e che anche le valutazioni sui possibili
esiti di
costante implica
che essa sia prefissata a priori e che anche le valutazioni sui possibili
esiti di 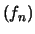 siano fatte prima di iniziare le prove (o in
condizione di incertezza sul loro esito).
siano fatte prima di iniziare le prove (o in
condizione di incertezza sul loro esito).
- Ciò nonostante, vedremo come la frequenza relativa di
prove effettuate possa essere utilizzata per valutare
 ,
ma questo è un problema inferenziale che c'entra poco con il
teorema di Bernoulli (il
quale ha a che vedere, per dirla alla buona, soltanto con
``affermazioni probabilistiche su frequenza
relative future, o comunque ignote'').
,
ma questo è un problema inferenziale che c'entra poco con il
teorema di Bernoulli (il
quale ha a che vedere, per dirla alla buona, soltanto con
``affermazioni probabilistiche su frequenza
relative future, o comunque ignote'').
Facciamo degli esempi pratici
Subsections




Next: Lancio di una moneta
Up: Legge dei grandi numeri
Previous: Limite della media aritmetica
Indice
Giulio D'Agostini
2001-04-02
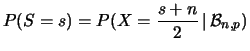
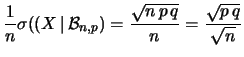
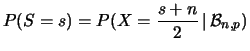
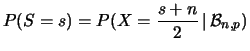
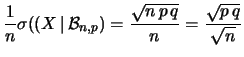
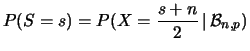
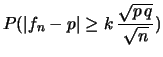
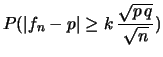
diventa sempre meno probabile osservare valori di frequenze relative che differiscono molto da
.
``tenda a
''] vengono ad assumere un ruolo di cerniera per convalidare tale avvicinamento o identificazione di nozioni. Logicamente non si sfugge però al dilemma che la stessa cosa non si può assumere prima per definizione e poi dimostrare come teorema, né alla contraddizione di una definizione che assumerebbe una cosa certa mentre il teorema afferma che è soltanto molto probabile.