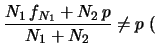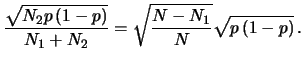Next: Teorema del limite centrale
Up: Teorema di Bernoulli
Previous: Lancio di una moneta
Indice
Assumiamo ora di avere un meccanismo di estrazione talmente
simmetrico da non avere nessun dubbio sulla probabilità di ciascuna
estrazione (ad esempio la ruota del lotto). Sia  tale probabilità
(ad esempio 1/90 per il primo estratto su una ruota).
Immaginiamo di interessarci ad
tale probabilità
(ad esempio 1/90 per il primo estratto su una ruota).
Immaginiamo di interessarci ad 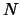 estrazioni e che dopo
estrazioni e che dopo
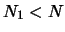 estrazioni (
estrazioni (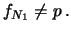 ) la frequenza relativa sia diversa
da
) la frequenza relativa sia diversa
da  (come in genere accade...):
Cosa ci aspettiamo sul totale delle
(come in genere accade...):
Cosa ci aspettiamo sul totale delle 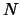 estrazioni
da eseguire?
estrazioni
da eseguire?
- -
- ci sarà un meccanismo di compensazione tale che
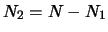 ?
?
- -
- Quanto vale il valore atteso della frequenza relativa
nelle restanti
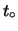 estrazioni e sul totale delle
estrazioni e sul totale delle 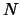 estrazioni?
estrazioni?
Queste sono le considerazioni probabilisticamente corrette all'istante
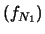 prima di iniziare le estrazioni e all'istante
prima di iniziare le estrazioni e all'istante 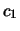 dopo che sono noti i risultati delle prime
dopo che sono noti i risultati delle prime
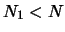 estrazioni:
estrazioni:
- a)
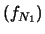 :
:
- siamo in stato di incertezza su ciascuno degli esiti.
Ne segue che
E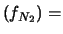 |
 |
E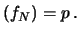 E E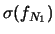 |
(10.54) |
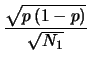 |
 |
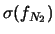 |
(10.55) |
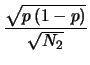 |
 |
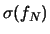 |
(10.56) |
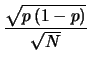 |
 |
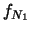 |
(10.57) |
- B)
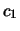 :
:
- il risultato
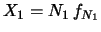 è acquisito (certo!). Esso
corrisponde a
è acquisito (certo!). Esso
corrisponde a
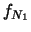 successi. Quindi:
successi. Quindi:
La previsione della frequenza è la media pesata fra  e la
frequenza nei primi
e la
frequenza nei primi 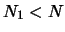 eventi. L'incertezza di previsione è massima
all'inizio (per
eventi. L'incertezza di previsione è massima
all'inizio (per 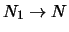 ) e va a zero per
) e va a zero per
 , in quanto
rimane poco su cui essere incerti.
, in quanto
rimane poco su cui essere incerti.
Lasciando al lettore tutte le conclusioni legate ai numeri ritardatari
e le raccomandazioni ai perdendi che ``contano'' di rifarsi
nelle partite successive, concludiamo con delle raccomandazioni.
I ragionamenti probabilistici vanno effettuati quando si è in
condizioni di incertezza. Si possono usare (vanno usate!)
le informazioni sulle frequenze osservate
per valutare le probabilità di altri eventi ignoti
nei modi che saranno visti quando
affronteremo in modo sistematico il
problema dell'inferenza statistica.
Utilizzare
argomentazioni probabilistiche su eventi noti non ha alcun senso.
Utilizzare poi tali argomentazioni allo stesso tempo sia su
eventi incerti che su eventi certi conduce ad una grossa confusione,
una di questa è
l'interpretazione distorta del teorema di Bernoulli.




Next: Teorema del limite centrale
Up: Teorema di Bernoulli
Previous: Lancio di una moneta
Indice
Giulio D'Agostini
2001-04-02