Nei paragrafi precedenti abbiamo imparato a valutare previsione e incertezza di previsione di combinazioni lineari di variabili casuali, indipendentemente dalla loro distribuzione. Ma per esprimere affermazioni probabilistiche su tali funzioni serve conoscere la distribuzione di probabilità e questo è un problema non banale (vedi paragrafi facoltativi 10.2 e 10.3). Comunque, l'esperienza su distribuzioni tipiche (vedi paragrafo 7.10) ci insegna che in genere c'è alta probabilità che in valore della variabile aleatoria cada entro alcune deviazioni standard dal valore atteso. Quando poi ci sono servite della considerazioni probabilistiche estreme, indipendentemente dalla distribuzione, abbiamo fatto uso della disuguaglianza di Cebicev.
In realtà le combinazioni lineari tendono ad avere una distribuzione di probabilità universale, indipendentemente dalle distribuzioni di partenza, come consequenza del teorema del limite centrale, che formularemo fra breve. Siccome consideriamo assolutamente facoltativa la dimostrazione del teorema e molto più importante una sua modellizzazione e rappresentazione visiva, cominciamo con degli esempi pratici.
Abbiamo visto nel capitolo 6
come costruire una variabile casuale sulla somma degli esiti
di due dadi. Mentre la distribuzione dell'esito
di un solo dado è uniforme, la distribuzione della somma
mostra un addenzamento della probabilià al centro, ed un massimo
in corrispondenza di ![]() . La
figura 6.2 mostra chiaramente l'origine
del cambiamento di forma: ci sono molte combinazioni
che possono dare valori centrali e poche che possono dare valori laterali.
Se si somma la variabile ``due dadi'' con un'altra variabile
indipendente legata ad un solo dado,
di nuovo sarà molto probabile formare combinazioni intorno al centro della
distribuzione (vedi ad esempio figura 10.1).
. La
figura 6.2 mostra chiaramente l'origine
del cambiamento di forma: ci sono molte combinazioni
che possono dare valori centrali e poche che possono dare valori laterali.
Se si somma la variabile ``due dadi'' con un'altra variabile
indipendente legata ad un solo dado,
di nuovo sarà molto probabile formare combinazioni intorno al centro della
distribuzione (vedi ad esempio figura 10.1).
Anche partendo da una distribuzione continua uniforme si ha lo stesso effetto: la somma di due variabili dà luogo ad una distribuzione triangolare (chi è interessato alla dimostrazione può consultare il paragrafo 10.3.3, ma anche la sola figura 10.3 è autoesplicativa e mostra l'analogia con il lancio dei dadi).
Osserviamo ora la figura 10.5. Essa mostra
le distribuzioni simulate ottenute estraendo un certo numero
di variabili casuali (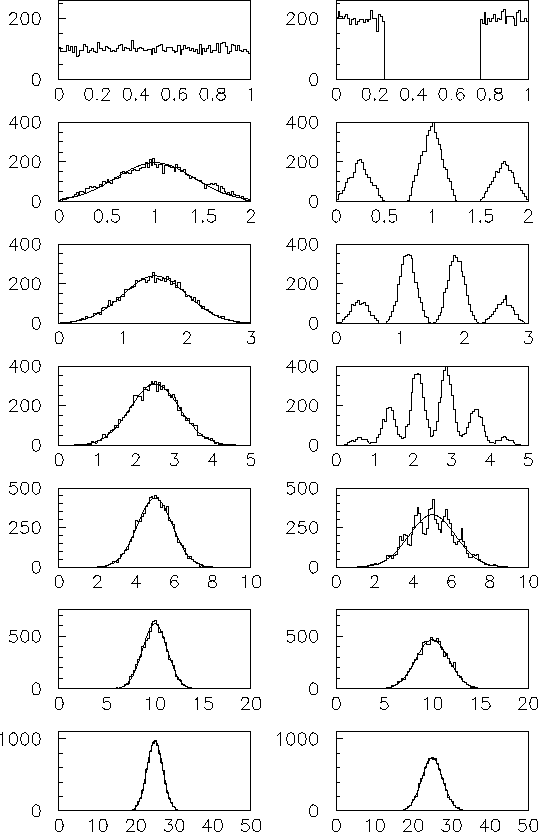 , 2, 3, 5, 10, 20 e 100) e sommandole
fra di loro. Questo processo è ripetuto 10000 volte.
Si ottiene quindi, per ciascun caso, una distribuzione statistica
che somiglia alla corrispondente distribuzione di
probabilità10.11. Le distribuzioni di base
sono una uniforme fra 0 e 1 e una distribuzione ``strana''
uniforme fra 0 e 0.25, fra 0.75 e 1, nulla altrove.
La distribuzione ``strana'' è particolarmente istruttiva per capire
l'effetto di addensamento al centro della probabilità dovuto
alle combinazione dei diversi valori. Ad esempio, per
, 2, 3, 5, 10, 20 e 100) e sommandole
fra di loro. Questo processo è ripetuto 10000 volte.
Si ottiene quindi, per ciascun caso, una distribuzione statistica
che somiglia alla corrispondente distribuzione di
probabilità10.11. Le distribuzioni di base
sono una uniforme fra 0 e 1 e una distribuzione ``strana''
uniforme fra 0 e 0.25, fra 0.75 e 1, nulla altrove.
La distribuzione ``strana'' è particolarmente istruttiva per capire
l'effetto di addensamento al centro della probabilità dovuto
alle combinazione dei diversi valori. Ad esempio, per ![]() ,
si nota un triangolo centrale doppio di ciascuno dei triangoli laterali.
Esso è dovuto alla probabilità che un
valore grande di una variabile si combini
con un valore grande dell'altra variabile.
,
si nota un triangolo centrale doppio di ciascuno dei triangoli laterali.
Esso è dovuto alla probabilità che un
valore grande di una variabile si combini
con un valore grande dell'altra variabile.
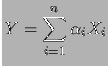 |
Si nota che, al crescere dei termini della sommatoria, la
distribuzione risultante ha una forma regolare a campana
indipendentemente dalla forma iniziale. Si noti come
le distribuzioni asintotiche (![]() ) sono
centrate sullo stesso valore in entrambi i casi,
mentre sono diverse le larghezze. Questa è consequenza che
le due distribuzioni
iniziali avessero stessa media, ma diversa deviazione standard
(quella ``strana'' indica una previsione del quadrato
degli scarti dalla media più
grande dell'altro caso). La curva riportata sui vari istogrammi
è una gaussiaana. Si vede come, da un certo
) sono
centrate sullo stesso valore in entrambi i casi,
mentre sono diverse le larghezze. Questa è consequenza che
le due distribuzioni
iniziali avessero stessa media, ma diversa deviazione standard
(quella ``strana'' indica una previsione del quadrato
degli scarti dalla media più
grande dell'altro caso). La curva riportata sui vari istogrammi
è una gaussiaana. Si vede come, da un certo ![]() in poi
(diverso per i due casi!) la distribuzione è ben approssimata da una
normale.
in poi
(diverso per i due casi!) la distribuzione è ben approssimata da una
normale.
Questo comportamento è dovuto al teorema del limite centrale:
datevariabili casuali indipendenti
, anche descritte da distribuzioni di probabilità diverse (purché aventi valore medio e varianza finiti), al crescere di
(``nel limite di
'') la combinazione lineare
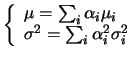
ha distribuzione di probabilità normale di parametri
purché sia
per ogni variabileÈ importante aggiungere delle note esplicative.non distribuita normalmente.