



Next: Somma di due variabili
Up: Somma di due variabili
Previous: Somma di due variabili
Indice
L'analogo continuo della somma dei due dadi di figura
10.1 è dado dalla somma di due variabili indipendenti
distribuite uniformemente, per semplicità nell'intervallo [0,a].
Sia
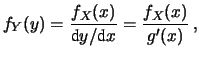 che
che
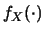 valgono
valgono 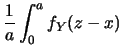 . Applicando la
(10.17) si ha:
. Applicando la
(10.17) si ha:
avendo eseguito, nell'ultimo passaggio, la
seguente
trasformazione di variabili:
Facendo attenzione a come gli estremi di integrazione della
(10.18) sono legati al dominio della
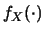 ,
si ottiene finalmente:
,
si ottiene finalmente:
 |
(10.19) |
Figura:
Costruzione delle distribuzioni di 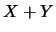 e di
e di 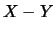 a partire da
a partire da  e
e  indipendenti e distribuite uniformemente
fra 0 e 1.
indipendenti e distribuite uniformemente
fra 0 e 1.
 |
Si riconosce una distribuzione triangolare (vedi paragrafo
8.4)
centrata in  e di
semiampiezza
e di
semiampiezza 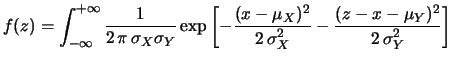 . Per capire in modo intuitivo questo andamento
si può confrontare questo risultato con quanto ottenuto nella somma
di due dadi (vedi figura 10.1). Si veda anche la figura
10.3 che mostra, per una distribuzione uniforme
fra 0 e 1 la distribuzione della somma e della differenza. Si vede
che, a parte la posizione del centro, tale combinazione dà luogo
alla stessa forma, quindi con uguale incertezza.
. Per capire in modo intuitivo questo andamento
si può confrontare questo risultato con quanto ottenuto nella somma
di due dadi (vedi figura 10.1). Si veda anche la figura
10.3 che mostra, per una distribuzione uniforme
fra 0 e 1 la distribuzione della somma e della differenza. Si vede
che, a parte la posizione del centro, tale combinazione dà luogo
alla stessa forma, quindi con uguale incertezza.




Next: Somma di due variabili
Up: Somma di due variabili
Previous: Somma di due variabili
Indice
Giulio D'Agostini
2001-04-02
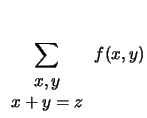
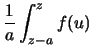 d
d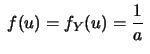
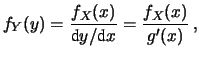 che
che
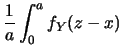 . Applicando la
(10.17) si ha:
. Applicando la
(10.17) si ha:
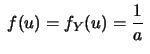
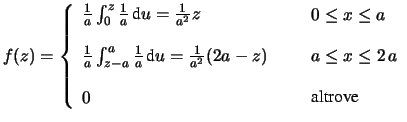

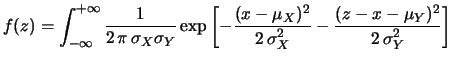 . Per capire in modo intuitivo questo andamento
si può confrontare questo risultato con quanto ottenuto nella somma
di due dadi (vedi figura 10.1). Si veda anche la figura
10.3 che mostra, per una distribuzione uniforme
fra 0 e 1 la distribuzione della somma e della differenza. Si vede
che, a parte la posizione del centro, tale combinazione dà luogo
alla stessa forma, quindi con uguale incertezza.
. Per capire in modo intuitivo questo andamento
si può confrontare questo risultato con quanto ottenuto nella somma
di due dadi (vedi figura 10.1). Si veda anche la figura
10.3 che mostra, per una distribuzione uniforme
fra 0 e 1 la distribuzione della somma e della differenza. Si vede
che, a parte la posizione del centro, tale combinazione dà luogo
alla stessa forma, quindi con uguale incertezza.