



Next: Esempio di applicazione alle
Up: Funzioni di variabili casuali
Previous: pzd100 Simulazione di numeri
Indice
Una conseguenza importante delle proprietà della combinazione
lineare e del teorema del limite centrale è la seguente:
se si hanno
delle variabili 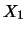 ,
, 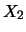 ,...
,...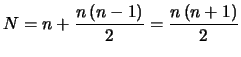 e una
variabile
e una
variabile  funzione arbitraria di esse, ovvero
che sia abbastanza lineare nell'intorno del valore atteso di
ciascuna delle
funzione arbitraria di esse, ovvero
che sia abbastanza lineare nell'intorno del valore atteso di
ciascuna delle  (ovvero
(ovvero 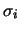 ) ove si addensa il grosso
della probabilità (ovvero entro qualche
) ove si addensa il grosso
della probabilità (ovvero entro qualche 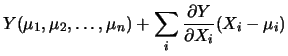 da
da 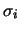 )
allora, espandendo
)
allora, espandendo  in serie di Taylor otteniamo
in serie di Taylor otteniamo
ove le derivate si intendono calcolate per 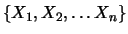 .
Il secondo modo di scrivere l'espansione, in cui sono stati
inglobati in
.
Il secondo modo di scrivere l'espansione, in cui sono stati
inglobati in  tutti i termini non dipendenti da
tutti i termini non dipendenti da  , mostra
chiaramente che la
, mostra
chiaramente che la  è una combinazione lineare
delle
è una combinazione lineare
delle  con coefficienti pari alle derivate calcolate
nella previsione del vettore aleatorio
con coefficienti pari alle derivate calcolate
nella previsione del vettore aleatorio
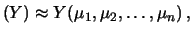 .
Si possono applicare quindi a questa combinazione lineare ed
ad altre combinazioni lineari costruite sulle
.
Si possono applicare quindi a questa combinazione lineare ed
ad altre combinazioni lineari costruite sulle  tutti
i teoremi incontrati in questo capitolo. In particolare, abbiamo:
tutti
i teoremi incontrati in questo capitolo. In particolare, abbiamo:




Next: Esempio di applicazione alle
Up: Funzioni di variabili casuali
Previous: pzd100 Simulazione di numeri
Indice
Giulio D'Agostini
2001-04-02
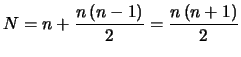 e una
variabile
e una
variabile 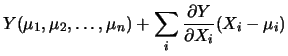 da
da 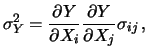 ;
;
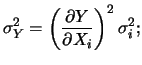
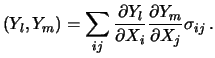 sono date
da
sono date
da