



Next: Moto browniano, ``pallinometro'' ed
Up: Funzioni di variabili casuali
Previous: Linearizzazione
Indice
Facciamo subito un esempio di come sia possibile applicare
le proprietà delle combinazioni lineari
e della linearizzazione alle incertezze di misure.
Anche se non è stato ancora affrontato il discorso dell'inferenza
statistica e di come si valutino le incertezze delle misure dirette
e le correlazioni introdotte da possibili errori sistematici
di entità incerta, supponiamo che siano stati misurati i due lati
di un rettangolo e che i risultati siano presentati in termini
di previsione e di incertezza di previsione:
Ripetendo quanto detto al momento di introdurre
previsione e incertezza e incertezza di previsione:
E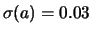 cm rappresenta il valore intorno al quale
riteniamo che, ragionevolmente, si trovi
cm rappresenta il valore intorno al quale
riteniamo che, ragionevolmente, si trovi  ;
;
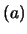 cm
indica la dispersione dei valori che possono essere assunti da
cm
indica la dispersione dei valori che possono essere assunti da  intorno ad
E
intorno ad
E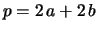 .
.
Immaginiamo di essere interessati ora alle seguenti grandezze derivate da
 e
e 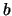 : perimetro (
: perimetro (
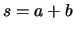 ); somma di lati (
); somma di lati (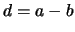 );
differenza dei lati (
);
differenza dei lati (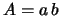 ); area del rettangolo (
); area del rettangolo (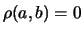 ).
Supponiamo inoltre i due casi: a) le misure di
).
Supponiamo inoltre i due casi: a) le misure di  e
e 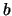 sono assolutamente
indipendenti, per cui
sono assolutamente
indipendenti, per cui
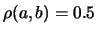 ; b) parziale correlazione, con
; b) parziale correlazione, con
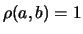 ; c) correlazione totale (positiva), con
; c) correlazione totale (positiva), con
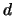 .
.
Si riconoscono in  ,
, 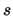 e
e 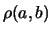 correlazioni lineari di
correlazioni lineari di  e
e 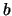 ,
mentre il caso dell'area è non lineare e va linearizzato.
Riportiamo nel seguito i risultati dettagliati per
,
mentre il caso dell'area è non lineare e va linearizzato.
Riportiamo nel seguito i risultati dettagliati per 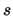 ,
, 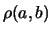 e
e  nei tre casi di correlazione considerati.
Innanzitutto, le previsioni di
nei tre casi di correlazione considerati.
Innanzitutto, le previsioni di 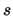 ,
, 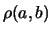 e
e  non dipendono da
non dipendono da 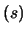 e valgono
e valgono
E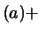 |
 |
E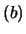 E E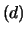 |
(10.67) |
E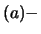 |
 |
E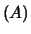 E E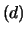 |
(10.68) |
E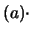 |
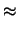 |
E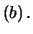 E E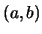 |
(10.69) |
Per quanto riguarda le varianze, ricordando che
Cov è pari a
è pari a
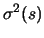 , abbiamo
, abbiamo
Si noti il simbolo ``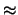 '' al posto di ``
'' al posto di ``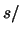 '' nel caso di
'' nel caso di  ,
per ricordare che si tratta di un risultato approssimato
basato sulla linearizzazione.
I risultati numerici sono:
,
per ricordare che si tratta di un risultato approssimato
basato sulla linearizzazione.
I risultati numerici sono:
Troviamo infine i coefficienti di correlazione fra 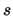 ,
, 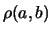 e
e  ,
come applicazione di quanto visto nel paragrafo
10.8. Utilizzando la formula
(10.45), svolgendo in dettaglio
il primo passaggio, otteniamo
,
come applicazione di quanto visto nel paragrafo
10.8. Utilizzando la formula
(10.45), svolgendo in dettaglio
il primo passaggio, otteniamo
ove, di nuovo, ``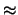 '' sta a ricordare che il risultato è
basato sulla linearizzazione.
Inserendo i valori e dividendo per le deviazione standard,
otteniamo direttamente i coefficienti di correlazione in funzione
di
'' sta a ricordare che il risultato è
basato sulla linearizzazione.
Inserendo i valori e dividendo per le deviazione standard,
otteniamo direttamente i coefficienti di correlazione in funzione
di 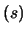 :
:
Si noti:
- il coefficiente di correlazione fra
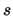 e
e 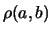 è nullo per puro accidente,
dovuto all'uguaglianza di
è nullo per puro accidente,
dovuto all'uguaglianza di 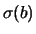 e
e 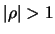 );
);
- per calcolare i coefficienti di correlazione per valori molto prossimi
ad 1, bisogna utilizzare molte cifre significative nel calcoli,
altrimenti si possono ottenere risultati assurdi (
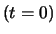 ) a causa
degli arrotondamenti;
) a causa
degli arrotondamenti;
- quando le funzioni diventano complicate non è facile
farsi un'idea intuitiva del grado di correlazione e
addirittura nemmeno del suo segno.




Next: Moto browniano, ``pallinometro'' ed
Up: Funzioni di variabili casuali
Previous: Linearizzazione
Indice
Giulio D'Agostini
2001-04-02
![]() e
e ![]() : perimetro (
: perimetro (
![]() ); somma di lati (
); somma di lati (![]() );
differenza dei lati (
);
differenza dei lati (![]() ); area del rettangolo (
); area del rettangolo (![]() ).
Supponiamo inoltre i due casi: a) le misure di
).
Supponiamo inoltre i due casi: a) le misure di ![]() e
e ![]() sono assolutamente
indipendenti, per cui
sono assolutamente
indipendenti, per cui
![]() ; b) parziale correlazione, con
; b) parziale correlazione, con
![]() ; c) correlazione totale (positiva), con
; c) correlazione totale (positiva), con
![]() .
.
![]() ,
, ![]() e
e ![]() correlazioni lineari di
correlazioni lineari di ![]() e
e ![]() ,
mentre il caso dell'area è non lineare e va linearizzato.
Riportiamo nel seguito i risultati dettagliati per
,
mentre il caso dell'area è non lineare e va linearizzato.
Riportiamo nel seguito i risultati dettagliati per ![]() ,
, ![]() e
e ![]() nei tre casi di correlazione considerati.
Innanzitutto, le previsioni di
nei tre casi di correlazione considerati.
Innanzitutto, le previsioni di ![]() ,
, ![]() e
e ![]() non dipendono da
non dipendono da ![]() e valgono
e valgono