Nel 1905 Albert Einstein pubblicò un articolo dal titolo
``Il moto delle particelle in sospensione nei fluidi in quiete,
come previsto dalla teoria cinetico-molecolare del calore''. In esso
diede una spiegazione in termini di teoria cinetica dei gas
del moto browniano, osservato per primo dal biologo Robert
Brown nel 1828 durante lo studio del comportamento di polline in soluzione
acquosa. È molto interessante leggere l'inizio dell'articolo10.12:
``In questo lavoro faremo vedere come, secondo la teoria cinetico-molecolare del calore, particelle in sospensione in una soluzione compiano, in consequenza del moto termico delle molecole, movimenti di ampiezza tale che li si può agevolmente osservare al microscopio, purché, beninteso, la dimensione delle particelle stesse sia accessibile allo strumento. Può darsi che i moti che qui saranno considerati coincidano con il cosiddetto moto molecolare browniano; tuttavia i dati che ho potuto ottenere su quest'ultimo sono così imprecisi che non mi è stato possibile formulare alcun giudizio in merito.
Se il moto in questione si potrà effettivamente osservare, con tutte le regolarità che per esso si possono attendere, la termodinamica classica non sarà più da considerare esattamente valida già per spazi microscopicamente distinguibili, e quindi una determinazione esatta della vera grandezza degli atomi sarà possibile. Se viceversa la nostra previsione si dimostrasse inesatta, ciò fornirebbe un serio argomento contro la concezione cinetico-molecolare del calore''.Il moto browniano viene quindi interpretato come una conseguenza del moto disordinato delle particelle a seguito degli urti che ricevono dalle molecole sottoposte ad agitazione termica. Nella trattazione ogni particella viene considerata indipendentemente dalle altre. Il risultato di Einstein fu - prendendo per semplicità il caso unidimensionale - che dopo un certo intervallo di tempo
``La distribuzione di frequenza delle variazioni di posizione avvenute in un tempo t arbitrario coincide dunque con quella degli errori casuali, come ci si poteva attendere.''Ci possiamo ricavare lo stesso risultato seguendo un approccio basato sul cosiddetto moto casuale: schematizziamo il moto browniano come un moto casuale di una pedina che, partendo all'istante iniziale dalla posizione iniziale
Per utilizzare la stessa notazione del paragrafo 2.9 della seconda parte di queste dispense consideriamo degli intervalli di tempo
| E |
0 | ||
| Var |
| E |
0 | (10.78) | |
| Var |
(10.79) | ||
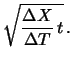 |
(10.80) |
A questo punto vale la pena di sottolineare la relazione fra teorema del limite centrale, moto browniano e distribuzione degli errori casuali di misura. Il risultato di ogni singola misura può essere pensato come dovuto a tanti piccoli contributi incoerenti e non controllabili dallo sperimentatore, ognuno dei quali tende a modificare il risultato, in modo del tutto casuale, in un verso o nell'altro. Si pensi ad esempio a vibrazioni, attriti, variazioni termiche, rumore elettronico etc. I vari contributi modificano il valore ideale della grandezza da misurare, il quale viene a compiere una specie di moto browniano in uno spazio astratto. In virtù di questa variazione casuale della grandezza fisica, la singola misura di uno strumento ha la tendenza ad avere errori di tipo normale. In genere essa viene mediata con altri risultati. Infine i risultati delle misure di più grandezze possono venire combinati per ottenere, attraverso relazioni funzionali, altre grandezze fisiche. Si comprende quindi il motivo per il quale all'aumentare del numero di passaggi gli errori tendono sempre più ad assumere una distribuzione normale.