



Next: Problemi
Up: Funzioni di variabili casuali
Previous: Moto browniano, ``pallinometro'' ed
Indice
Come altro esempio di applicazione della
distribuzione
normale, ricaviamo
la distribuzione di velocità di un gas perfetto, a partire da un
moto browniano nello spazio dei momenti. Supponiamo di
avere una molecola inizialmente
immobile in un recipiente pieno di gas e consideriamo
la componente lungo l'asse  della velocità.
della velocità.
- se supponiamo che ad ogni urto la particella
acquisti una certa velocità
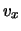 possiamo immaginare
di ottenere un moto browniano in
possiamo immaginare
di ottenere un moto browniano in 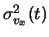 la cui soluzione
sarà, come abbiamo visto, una gaussiana di media nulla e
varianza
la cui soluzione
sarà, come abbiamo visto, una gaussiana di media nulla e
varianza
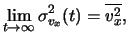 ;
;
-
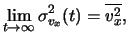 non può andare all'infinito. Superata una
certa velocità media (in modulo) la probabilità che la molecola
perda energia è maggiore di quella che ne acquisti. La condizione di
equilibrio termodinamico è che, passato un tempo
sufficientemente grande, tutte le
molecole sono
descritte dalla stessa distribuzione di probabilità
delle velocità, e in particolare:
dove
non può andare all'infinito. Superata una
certa velocità media (in modulo) la probabilità che la molecola
perda energia è maggiore di quella che ne acquisti. La condizione di
equilibrio termodinamico è che, passato un tempo
sufficientemente grande, tutte le
molecole sono
descritte dalla stessa distribuzione di probabilità
delle velocità, e in particolare:
dove
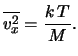 è la velocità quadratica media che si ottiene
dalla teoria cinetica dei gas:
è la velocità quadratica media che si ottiene
dalla teoria cinetica dei gas:
Il risultato è:
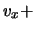 d
d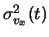 dà la probabilità di trovare la molecola con velocità
compresa fra
dà la probabilità di trovare la molecola con velocità
compresa fra 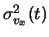 e
e
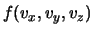 d
d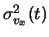 . Essendo i movimenti della
molecola sui tre assi indipendenti l'uno dall'altro otteniamo che la
probabilità congiunta è pari al prodotto delle probabilità:
. Essendo i movimenti della
molecola sui tre assi indipendenti l'uno dall'altro otteniamo che la
probabilità congiunta è pari al prodotto delle probabilità:
Negli ultimi passaggi siamo passati al modulo delle velocità 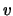 attraverso
d
attraverso
d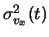 d
d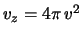 d
d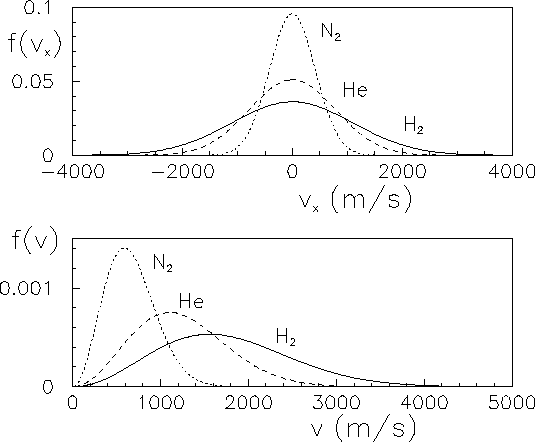 d
d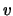 (passaggio da coordinate cartesiane a
coordinate polari). Abbiamo così riottenuto in un modo euristico
la distribuzione di Maxwell delle velocità, verificando in tal
modo che ciascuna delle componenti della velocità ha una
distribuzione di probabilità normale.
La Fig. 10.9 mostra le distribuzioni di probabilità del
modulo della velocità e di una delle sua componenti per alcune
molecole a temperatura ambiente.
(passaggio da coordinate cartesiane a
coordinate polari). Abbiamo così riottenuto in un modo euristico
la distribuzione di Maxwell delle velocità, verificando in tal
modo che ciascuna delle componenti della velocità ha una
distribuzione di probabilità normale.
La Fig. 10.9 mostra le distribuzioni di probabilità del
modulo della velocità e di una delle sua componenti per alcune
molecole a temperatura ambiente.
Figura:
Distribuzione di velocità delle molecole di un gas
perfetto
 |




Next: Problemi
Up: Funzioni di variabili casuali
Previous: Moto browniano, ``pallinometro'' ed
Indice
Giulio D'Agostini
2001-04-02
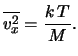 è la velocità quadratica media che si ottiene
dalla teoria cinetica dei gas:
è la velocità quadratica media che si ottiene
dalla teoria cinetica dei gas:
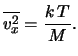 è la velocità quadratica media che si ottiene
dalla teoria cinetica dei gas:
è la velocità quadratica media che si ottiene
dalla teoria cinetica dei gas:
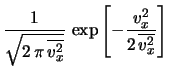
![$\displaystyle \frac{1}{\sqrt{2\, \pi\, \overline{v_x^2}}}
\, \exp{\left[-\frac{v_x^2}{2\, \overline{v_x^2}}\right]}$](img3141.png)
![$\displaystyle \frac{1}{\sqrt{2\pi\, \frac{k\, T}{m}}}
\,\exp{\left[-\frac{v_x^2}{2\, \frac{k\, T}{m}}\right]}$](img3142.png)
![]() d
d![]() dà la probabilità di trovare la molecola con velocità
compresa fra
dà la probabilità di trovare la molecola con velocità
compresa fra ![]() e
e
![]() d
d![]() . Essendo i movimenti della
molecola sui tre assi indipendenti l'uno dall'altro otteniamo che la
probabilità congiunta è pari al prodotto delle probabilità:
. Essendo i movimenti della
molecola sui tre assi indipendenti l'uno dall'altro otteniamo che la
probabilità congiunta è pari al prodotto delle probabilità:
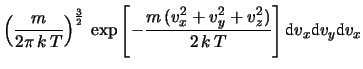 d
d![$\displaystyle \left(\frac{m}{2\pi\, k\, T}\right)^{\frac{3}{2}}
\, \exp{\left[-...
...\, (v_x^2+v_y^2+v_z^2)}
{2\, k\, T}\right]}\,
\mbox{d}v_x\mbox{d}v_y\mbox{d}v_x$](img3151.png)
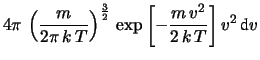 d
d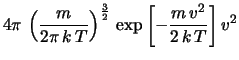
![$\displaystyle 4\pi\, \left(\frac{m}{2\pi\, k\, T}\right)^{\frac{3}{2}}
\, \exp{\left[-\frac{m\, v^2}{2\, k\, T}
\right]}\, v^2$](img3156.png)
 d
d