${\bf\circlearrowright\,}$ Speranza matematica e previsione di vincita

Il concetto della scommessa reversibile può essere ribadito pensando che se si è incerti se puntare pro o contro l'evento $E$ - almeno dal punto di vista ipotetico - significa che $A$ e $P(E)\cdot S$ vengono considerati di pari valore e quindi interscambiabili: si può versare la cifra ``sicura'' $A$ con la speranza di poter ottenere $S$ con probabilità $P(E)$ (se $E$ si verifica); indifferentemente si può accettare la cifra sicura $A$ con il rischio di pagare $S$ con probabilità $P(E)$.

Siccome non sempre le scommesse sono eque, è interessante chiamare speranza matematica (di vincita), o valore atteso (di vincita), la somma che si spera di vincere per la probabilità di vincita. Chiamiamo questa quantità $M (= P(E)\cdot S)$, per distinguerla dalla generica posta $A$ che chi organizza il gioco può richiedere di pagare. Se $A$ è uguale a $M$ il gioco è equo. Quindi il rapporto $A/M$ caratterizza l'equità del gioco. Facciamo degli esempi.

• Roulette^2.13, giocando al ``rosso e nero'' (ad esempio $E$= ``rosso''):
  

  $$P(E) = \frac{18}{37}$$

  $$S = 2\, A$$

  $$\frac{M}{A} = \frac{36}{37} = 0.973 \ (97.3\,\%) \,.$$

  
  
  Il gioco è evidentemente non equo, ma non troppo sbilanciato.
• Roulette, puntando su un numero (es. $E$ = ``esce il 24''):
  

  $$P(E) = \frac{1}{37}$$

  $$S = 36\, A$$

  $$\frac{M}{A} = \frac{36}{37} = 0.973 \ (97.3\,\%) \,.$$

  
  
  In effetti tutte le vincite della roulette sono calcolate in modo tale da mantenere un rapporto costante fra puntata e speranza matematica.
• Lotto, puntando su un numero su una ruota (es. $E$ = ``esce il 25 sulla ruota di Bari''):
  

  $$P(E) = \frac{5}{90} = \frac{1}{18}$$

  $$S = 10.9\, A$$

  $$\frac{M}{A} = \frac{10.9}{18} = 0.605 \ (60.5\,\%) \,.$$

  
  
  Il banco del lotto vince mediamente quasi il 40% delle puntate^2.14, contro il 2.7 di quello della roulette.

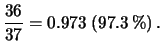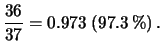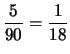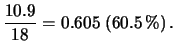Come si vede, la conoscenza della speranza matematica permette di giudicare l'equità di un gioco d'azzardo, cioè caratterizza il gioco, anche senza che se ne conoscano in dettaglio le regole. Si vede, ad esempio, che il gioco della roulette è molto più equo del lotto. Anzi si potrebbe dire per inciso che sembra anche ``troppo equo'', nel senso che la speranza matematica differisce soltanto del 2.7% dalla puntata. Presumibilmente bisogna tener conto che, anche se il gioco è quasi equo dal punto di vista probabilistico, non lo è dal punto di vista psicologico, e infatti quasi sempre i giocatori seguitano a giocare anche dopo che hanno vinto, e spesso finiscono per perdere tutta la cifra che erano disposti a giocare e sono costretti a smettere (esiste un classico problema del calcolo delle probabilità detto della ``rovina del giocatore'').