pzd100Ruolo virtuale della scommessa, valore dei soldi e ordini di grandezza non intuitivamente percepibili

Qualcuno può avere difficoltà ad accettare il ruolo della scommessa nelle valutazioni di probabilità per ragioni assolutamente legittime e quindi sono necessari alcuni chiarimenti, oltre a quelli appena dati.

Tipiche obiezioni possono essere:

a)

con chi bisogna scommettere?

b)

devo sempre fare scommesse coerenti?

c)

anche se ritenessi che la probabilità sia del 99.999% non accetterei mai di scommettere $99^\cdot999^\cdot000$ lire contro 1000 lire;

d)

intuitivamente posso ritenere che la probabilità sia molto bassa ( $\approx 1\,\%$), bassa ( $\approx 10$-$20\,\%$), media ( $\approx 40$-$60\,\%$), alta ( $\approx 80$-$90\,\%$) o molto alta ( $\approx 99\,\%$), ma come si può decidere se è 43 o 44%? O se è 99.9 invece di 99.9999%?

Cerchiamo di rispondere brevemente.

a)

La scommessa coerente deve essere intesa come operazionale, sebbene a livello ipotetico. Questo caso non è unico nella scienza.

-

Anche la definizione di sostanza velenosa è definita come ``letale se ingerita'', ma non si richiede una prova per ogni sostanza definita tale.

-

Un campo elettrico è definito dalla forza per unità di carica, ma sicuramente questo non è il modo di valutare il campo elettrico in prossimità di un elettrone.

Il ruolo normativo della scommessa coerente dovrebbe obbligare chi valuta la probabilità ad essere onesto con sé stesso e con la comunità scientifica. Ad esempio, se uno sperimentatore dichiara che il valore di una grandezza è compreso in un certo intervallo con probabilità del 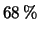$68\,\%$^2.11 dovrebbe essere disposto ad accettare una scommessa di circa 2 a 1 in favore di tale evento, e 1 a 2 contro. Se egli si sente pronto a scommettere pro ma è riluttante a scommettere contro vuol dire che crede in tale risultato molto di più del 68% dichiarato.

b)

Le scommesse coerenti servono solo per valutare la probabilità. Poi nella vita (a parte le tombolate natalizie con i familiari) si fanno scommesse non eque con l'intento di vincere. Però è opportuno stimare al meglio la probabilità per cercare di puntare meno della posta equa se si gioca pro, o far puntare di più se si sta dalla parte del banco.

Questo è quello che fanno gli allibratori professionisti, chi organizza lotto e lotterie nazionali, chi propone polizze assicurative, ma anche chi gioca semplicemente a scacchi o a scopone con gli amici. Che invece le valutazioni di chi segue i ``sistemi per vincere al lotto'' siano sbagliate è ``dimostrato'' sia dai guadagni che lo Stato fa su tali scommesse sia dal dato di fatto che i furbi, quando possono, si mettono a gestire lotterie clandestine e non di certo a giocare...

c)

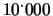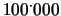Se si propone ad una persona razionale di giocare ai dadi alla pari $10^\cdot000$ o $100^\cdot000$ lire puntando contro il ``6'', questa riterrà l'offerta assolutamente vantaggiosa e non esiterà a giocare (a meno che non sospetti qualche trucco, vista l'enorme differenza dal rapporto equo delle puntate). Se però si propone una puntata che corrisponde a qualche anno di stipendio, o alla casa, pur mantenendo la scommessa alla pari, la maggior parte delle persone riterranno la scommessa inaccettabile. La probabilità di 1/6 di ``perdere tutto'' vince la tentazione di provare a raddoppiare con probabilità 5/6. Questo è dovuto al fatto che ``il valore dei soldi'' non è lo stesso per tutte le persone e sicuramente non è percepito in modo lineare^2.12. In risposta a questa obiezione vale quanto detto a proposito della lettura in chiave ipotetica della scommessa.

È da notare comunque che scommesse di questo tipo sono comunemente accettate da gestori di lotterie e da assicurazioni (anche se per ovvi motivi con ``puntate'' non eque) abbastanza coperti finanziariamente da poter affrontare il rischio di momentanee ``sovrafluttuazioni di sfortuna''.

d)

In effetti è vero che la probabilità soggettiva valutata in modo semplicemente intuitivo è rozza, e non potrebbe essere altrimenti. Ma vedremo dei metodi che permetteranno, a partire da stime approssimative, di riaggiornare la probabilità ottenendo valori spesso ben precisi. Questi metodi stanno ai calibri come la percezione intuitiva di probabilità sta a quella di spazio. La stessa analogia vale per valori di probabilità molti prossimi a uno o a zero. Situazioni analoghe nel dominio dello spazio sono le distanze astronomiche o nucleari.

A questo proposito hanno un ruolo importante i semplici problemi delle urne con palline bianche e nere, oppure con numeri casuali distribuiti uniformemente fra 0 e 1. Essi rappresentano delle scale ``oggettive'' di probabilità (leggi: ``sulle quali non possiamo non essere tutti d'accordo'') con le quali confrontare valutazioni puramente intuitive. Quindi una probabilità del 70% dovrebbe dare circa la stessa sicurezza di quando si spera di poter estrarre una pallina bianca da un'urna che contiene 70 palline bianche e 30 palline nere. Se questo non è vero vuol dire che 70% non corrisponde all'effettiva credibilità dell'evento.