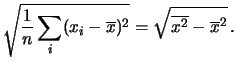Next: Possibili dubbi sul modello
Up: Caso di ignota
Previous: Caso di ignota
Indice
Ragionamento intuitivo
Il modo più semplice di ragionare, senz'altro valido
quando  è abbastanza grande, è il seguente.
è abbastanza grande, è il seguente.
- Abbiamo visto che,
assumendo il parametro
 identico in tutte le oservazioni,
la previsione di
E
identico in tutte le oservazioni,
la previsione di
E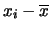 è uguale alla media aritmetica,
indipendentemente dal valore di
è uguale alla media aritmetica,
indipendentemente dal valore di  , con incertezza di
previsione
, con incertezza di
previsione
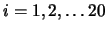 .
.
- Possiamo allora dire che il valore vero di
 sia
approssimativamente
sia
approssimativamente
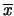 , e quindi gli scarti
, e quindi gli scarti
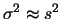 siano circa uguali agli scarti delle
osservazioni dal valore vero.
siano circa uguali agli scarti delle
osservazioni dal valore vero.
- La media dei quadrati degli scarti rispetto alla media
è, di consequenza, approssimativamente ugale alla media
degli scarti rispetto al valore vero, ovvero
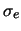 .
.
In conclusione, abbiamo
E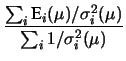 |
 |
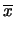 |
(11.53) |
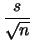 |
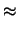 |
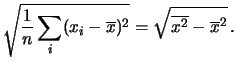 |
(11.54) |
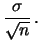 |
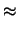 |
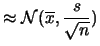 |
(11.55) |
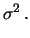 |
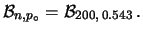 |
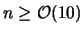 |
(11.56) |
Si noti il simbolo ``='' per la prima uguaglianza e ``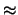 ''
per le altre. In fatti mentre l'espressione della previsione
di
''
per le altre. In fatti mentre l'espressione della previsione
di  è ``esatta'' (nel senso di previsione probabilistica
e con la sua incertezza) le alte dipendono dall'incertezza
di previsione di
è ``esatta'' (nel senso di previsione probabilistica
e con la sua incertezza) le alte dipendono dall'incertezza
di previsione di  e quindi sono ``esatte'' soltanto nel
caso di
e quindi sono ``esatte'' soltanto nel
caso di  ``molto grande''. Nel seguito vedremo, più
formalmente, l'origine e il limite di queste approssimazioni.
Per ora possiamo assicurare che questo ragionamento va
abbastanza bene, ai fini dei risultati quantitativi e
interessandoci soltanto alla ragione di
``molto grande''. Nel seguito vedremo, più
formalmente, l'origine e il limite di queste approssimazioni.
Per ora possiamo assicurare che questo ragionamento va
abbastanza bene, ai fini dei risultati quantitativi e
interessandoci soltanto alla ragione di  dove è condensata
la massa di probabilità, per
dove è condensata
la massa di probabilità, per
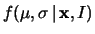 .
.




Next: Possibili dubbi sul modello
Up: Caso di ignota
Previous: Caso di ignota
Indice
Giulio D'Agostini
2001-04-02