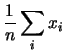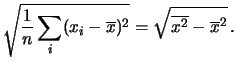Next: Ragionamento intuitivo
Up: Impostazione del problema. Caso
Previous: Correlazione fra i risultati
Indice
Nei paragrafi precedenti abbiamo assunto di avere
già delle idee sulla deviazione standard
del modello gaussiano di verosimiglianza.
Ovvero, ci siamo posti nelle condizioni di
avere già acquisito una certa esperienza,
o comunque una certa confidenza, sul comportamento
della singola osservazione (o osservazione equivalente).
È preferibile parlare, in termini generali, di confidenza
piuttosto che di esperienza, in quanto il nostro modello
(e i sui parametri) possono derivare, e è spesso il caso,
da simulazioni, estrapolazioni e analogie, piuttosto che
da una vera sperimentazione su quella grandezza fisica,
in quell'intervallo di valori possibili e
in quelle condizioni sperimentali.
Vediamo ora come valutare  del modello gaussiano
avendo registrato
del modello gaussiano
avendo registrato  osservazioni in condizioni
apparentemente identiche (nei limiti di un controllo reale
dell'esperimento e non dal punto di vista di un
diavoletto di Maxwell in grado di percepire qualsiasi
variazione microspopica) e avendo osservato una dispersione
di valori, intorno a un valore medio
osservazioni in condizioni
apparentemente identiche (nei limiti di un controllo reale
dell'esperimento e non dal punto di vista di un
diavoletto di Maxwell in grado di percepire qualsiasi
variazione microspopica) e avendo osservato una dispersione
di valori, intorno a un valore medio
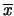 .
Quantifichiamo la dispersione dei valori con la deviazione
standard del campione statistico, che per evitare confusione
con il parametro
.
Quantifichiamo la dispersione dei valori con la deviazione
standard del campione statistico, che per evitare confusione
con il parametro  della gaussiana, chiameremo
della gaussiana, chiameremo 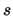 .
Abbiamo quindi:
.
Abbiamo quindi:
Avendo introdotto questi riassunti statistici del
campione in esame, procediamo per passi. Infatti questo
è uno degli argomenti
nei quali ci si può far prendere la mano dalla
matematica dimenticando il proprio stato di
conoscenza sulla natura delle cose e facendo perdere di mira
gli obiettivi pratici.
Subsections




Next: Ragionamento intuitivo
Up: Impostazione del problema. Caso
Previous: Correlazione fra i risultati
Indice
Giulio D'Agostini
2001-04-02