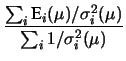Next: Prior uniforme in
Up: pzd100Inferenza simultanea su e
Previous: pzd100Inferenza simultanea su e
Indice
Come per  , il primo modello matematicamente
semplice di vaghezza che salta
in mente è una distribuzione uniforme per valori positivi
di
, il primo modello matematicamente
semplice di vaghezza che salta
in mente è una distribuzione uniforme per valori positivi
di  . Ovviamente, questo modello va preso
con cautela, come anche nel caso di
. Ovviamente, questo modello va preso
con cautela, come anche nel caso di  , in quanto
certamente non crediamo allo stesso modo a tutti i valori
di
, in quanto
certamente non crediamo allo stesso modo a tutti i valori
di  , specialmente quelli molto prossimi a zero
o che tendono a infinito (rispetto alla scala che abbiamo in mente
di valori plausibili). Dal modello otteniamo (assumendo implicito
il condizionante di contorno
, specialmente quelli molto prossimi a zero
o che tendono a infinito (rispetto alla scala che abbiamo in mente
di valori plausibili). Dal modello otteniamo (assumendo implicito
il condizionante di contorno 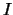 ):
):
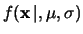 |
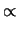 |
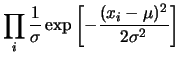 |
(11.62) |
| |
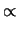 |
![$\displaystyle \prod_i \frac{1}{\sigma}
\exp{\left[-\frac{(x_i-\mu)^2}{2\sigma^2}\right]}$](img3382.png) |
(11.63) |
| |
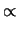 |
![$\displaystyle \sigma^{-n}\exp{\left[-\frac{1}{2\sigma^2}
\sum_i(x_i-\mu)^2\right]}$](img3383.png) |
(11.64) |
| |
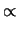 |
![$\displaystyle \sigma^{-n}\exp{\left[-\frac{1}{2\sigma^2}
\left( n\,(\overline{x}-\mu)^2+
n\,s^2
\right)\right]}\,,$](img3384.png) |
(11.65) |
ove nell'ultimo passaggio abbiamo utilizzato l'uguaglianza
con 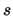 pari alla deviazione standard calcolata sui dati sperimentali:
pari alla deviazione standard calcolata sui dati sperimentali:
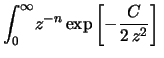 |
(11.66) |
Marginalizzando su  abbiamo:
11.7
abbiamo:
11.7
Avendo moltiplicato e diviso 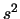 per
per 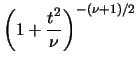 , si
riconosce una forma del tipo
, si
riconosce una forma del tipo
| |
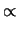 |
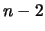 |
(11.68) |
con
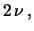 |
 |
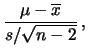 |
(11.69) |
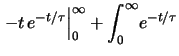 |
 |
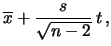 |
(11.70) |
ovvero |
|
|
|
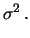 |
 |
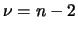 |
(11.71) |
ove  è la variabile
è la variabile  di Student con
di Student con 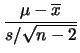 .
Applicando le note proprietà della distribuzione
di Student (vedi paragrafo 8.15.4 ), otteniamo:
.
Applicando le note proprietà della distribuzione
di Student (vedi paragrafo 8.15.4 ), otteniamo:
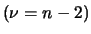 |
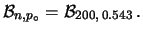 |
Student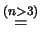 |
(11.72) |
E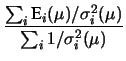 |
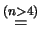 |
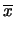 |
(11.73) |
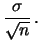 |
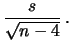 |
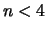 |
(11.74) |
Come si vede, l'incertezza su  produce una ulteriore
incertezza su
produce una ulteriore
incertezza su  , tale da rendere più plausibili valori
molto lontani dalla media (caratteristica delle
, tale da rendere più plausibili valori
molto lontani dalla media (caratteristica delle  di Student
rispetto alla normale standardizzata). Questo effetto è,
come è ragionevole che sia, più importante per
di Student
rispetto alla normale standardizzata). Questo effetto è,
come è ragionevole che sia, più importante per  piccolo
e si attenua immediatamente quando
piccolo
e si attenua immediatamente quando  supera il valore di qualche
decina. Per
supera il valore di qualche
decina. Per  al di sotto di
al di sotto di  le code della distribuzione
sono talmente pronunciate che la varianza è infinita e per
le code della distribuzione
sono talmente pronunciate che la varianza è infinita e per 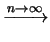 è addirittura il calcolo della media a non convergere.
Questo va bene dal punto di vista matematico, ma non
vuol dire che ``non si può dire niente su
è addirittura il calcolo della media a non convergere.
Questo va bene dal punto di vista matematico, ma non
vuol dire che ``non si può dire niente su  ''. Queste
divergenze non sono altro che il risultato della
ipersemplicità del modello. Nessuna persona ragionevole
crederà mai che avendo letto su un voltmetro 6.25 V,
6.32 V e 6.29 V crederà mai che il valore vero della tensione
sia compatibile con valori ``infiniti'', sia positivi che negativi
(è quello che ci dice la
''. Queste
divergenze non sono altro che il risultato della
ipersemplicità del modello. Nessuna persona ragionevole
crederà mai che avendo letto su un voltmetro 6.25 V,
6.32 V e 6.29 V crederà mai che il valore vero della tensione
sia compatibile con valori ``infiniti'', sia positivi che negativi
(è quello che ci dice la  di Student, e anche la più
tranquilla gaussiana, seppur con gli infiniti
``un po' meno probabili'', per dirla alla buona).
di Student, e anche la più
tranquilla gaussiana, seppur con gli infiniti
``un po' meno probabili'', per dirla alla buona).
Quando  diventa molto grande otteniamo gli stessi
risultati delle argomentazioni intuitive discusse
precedentemente (basate giustappunto su tale limite):
diventa molto grande otteniamo gli stessi
risultati delle argomentazioni intuitive discusse
precedentemente (basate giustappunto su tale limite):
E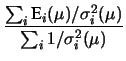 |
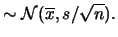 |
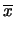 |
(11.75) |
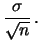 |
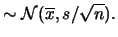 |
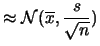 |
(11.76) |
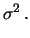 |
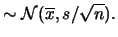 |
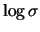 |
(11.77) |
Seguitiamo ora con questa parte formale, ritornando
successivamente a raccomandazioni su come comportarsi
in pratica.




Next: Prior uniforme in
Up: pzd100Inferenza simultanea su e
Previous: pzd100Inferenza simultanea su e
Indice
Giulio D'Agostini
2001-04-02
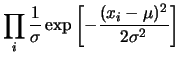
![$\displaystyle \prod_i \frac{1}{\sigma}
\exp{\left[-\frac{(x_i-\mu)^2}{2\sigma^2}\right]}$](img3382.png)
![$\displaystyle \sigma^{-n}\exp{\left[-\frac{1}{2\sigma^2}
\sum_i(x_i-\mu)^2\right]}$](img3383.png)
![$\displaystyle \sigma^{-n}\exp{\left[-\frac{1}{2\sigma^2}
\left( n\,(\overline{x}-\mu)^2+
n\,s^2
\right)\right]}\,,$](img3384.png)
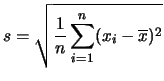
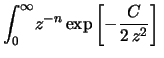
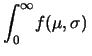
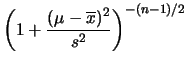
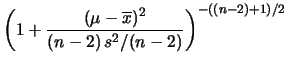
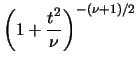 , si
riconosce una forma del tipo
, si
riconosce una forma del tipo
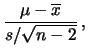
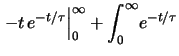
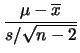 .
Applicando le note proprietà della distribuzione
di Student (vedi paragrafo 8.15.4 ), otteniamo:
.
Applicando le note proprietà della distribuzione
di Student (vedi paragrafo 8.15.4 ), otteniamo:
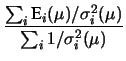
![]() diventa molto grande otteniamo gli stessi
risultati delle argomentazioni intuitive discusse
precedentemente (basate giustappunto su tale limite):
diventa molto grande otteniamo gli stessi
risultati delle argomentazioni intuitive discusse
precedentemente (basate giustappunto su tale limite):