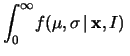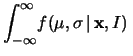Next: Prior uniforme in
Up: Caso di ignota
Previous: Possibili dubbi sul modello
Indice
pzd100Inferenza simultanea
su  e
e 
Affrontiamo ora il problema dal punto di vista generale.
Per inferire  e
e  da un insieme di
da un insieme di  osservazioni
che riteniamo indipendenti (condizionatamente ad ogni
ipotesi di
osservazioni
che riteniamo indipendenti (condizionatamente ad ogni
ipotesi di  e
e  ) e descritte da verosimiglianza
normale, dobbiamo semplicemente applicare il teorema di Bayes
a due numeri incerti anziché ad uno solo. Successivamente
si tratta di marginalizzare la distribuzione congiunta
sulla variabile che non ci interessa:
) e descritte da verosimiglianza
normale, dobbiamo semplicemente applicare il teorema di Bayes
a due numeri incerti anziché ad uno solo. Successivamente
si tratta di marginalizzare la distribuzione congiunta
sulla variabile che non ci interessa:
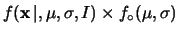 |
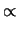 |
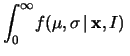 |
(11.57) |
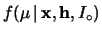 |
 |
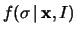 d d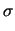 |
(11.58) |
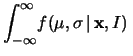 |
 |
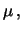 d d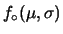 |
(11.59) |
ove abbiamo ricordato, ancora una volta, che tutta l'inferenza
dipende da tutte le condizioni di contorno 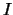 .
Come al solito cè il ``problema'' di che prior utilizzare.
Senza ripetere il lungo discorso
fatto a proposito di
.
Come al solito cè il ``problema'' di che prior utilizzare.
Senza ripetere il lungo discorso
fatto a proposito di  , è chiaro
che
, è chiaro
che
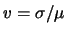 dovrebbe modellizzare, pur nella
sua vaghezza, quello che ci si aspetta su
dovrebbe modellizzare, pur nella
sua vaghezza, quello che ci si aspetta su  e
e  .
In alcune misure si è abbastanza
sicuri l'ordine di grandezza della deviazione
standard (``si è stupiti se venisse oltre
un valore di un ordine di grandezza in più o in meno di quanto
ci si aspetta). In altre misure si aspettano valori che possono
differire ``tranquillamente''
di uno o due ordini di grandezza rispetto a quello atteso,
ma quasi certamente non di un fattore 1000 o più.
In altri tipi di misure, forse è il caso più generale,
le aspettazioni sull'ordine di grandezza
non sono su
.
In alcune misure si è abbastanza
sicuri l'ordine di grandezza della deviazione
standard (``si è stupiti se venisse oltre
un valore di un ordine di grandezza in più o in meno di quanto
ci si aspetta). In altre misure si aspettano valori che possono
differire ``tranquillamente''
di uno o due ordini di grandezza rispetto a quello atteso,
ma quasi certamente non di un fattore 1000 o più.
In altri tipi di misure, forse è il caso più generale,
le aspettazioni sull'ordine di grandezza
non sono su  ma sul
coefficiente di variazione
ma sul
coefficiente di variazione
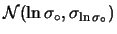 , ovvero sulla precisione,
in modo largamente indipendente dal valore
, ovvero sulla precisione,
in modo largamente indipendente dal valore  . E, infatti,
le misure vengono classificate in ``come ordine di grandezza'',
``al percento'', ``al per mille'', e così via.
Quindi,
ricordando che incertezza sull'ordine di grandezza significa
incertezza sul logaritmo della variabile, otteniamo le seguenti
possibilità:
. E, infatti,
le misure vengono classificate in ``come ordine di grandezza'',
``al percento'', ``al per mille'', e così via.
Quindi,
ricordando che incertezza sull'ordine di grandezza significa
incertezza sul logaritmo della variabile, otteniamo le seguenti
possibilità:
Si capisce come, una volta combinate queste
prior su  o su
o su 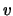 con quella
su
con quella
su  e inserite nella formula di Bayes,
i conti diventano complicati e, come veedremo, non vale
la pena di farli, a meno che non si tratti di un problema
cruciale. Vediamo un paio di modi di modellizzare la vaghezza
su
e inserite nella formula di Bayes,
i conti diventano complicati e, come veedremo, non vale
la pena di farli, a meno che non si tratti di un problema
cruciale. Vediamo un paio di modi di modellizzare la vaghezza
su  in modo da semplificare i conti e, in base
ai risultati ottenuti, di capire se vale la pena di
fare di meglio.
in modo da semplificare i conti e, in base
ai risultati ottenuti, di capire se vale la pena di
fare di meglio.
Subsections




Next: Prior uniforme in
Up: Caso di ignota
Previous: Possibili dubbi sul modello
Indice
Giulio D'Agostini
2001-04-02