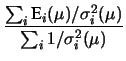Next: Incertezza su
Up: pzd100Inferenza simultanea su e
Previous: Prior uniforme in
Indice
Vediamo ora cosa succede se si sceglie una posizione
di assoluta indifferenza sugli ordini di grandezza di  ,
posizione assurda quanto quella precedente,
ma se non altro un po' più ragionevole della precedente e
con il vantaggio pratico di smorzare un po' gli eccessivamente
grandi valori di
,
posizione assurda quanto quella precedente,
ma se non altro un po' più ragionevole della precedente e
con il vantaggio pratico di smorzare un po' gli eccessivamente
grandi valori di  responsabili delle divergenze.
responsabili delle divergenze.
Assumere che
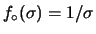 è equivalente
a
è equivalente
a
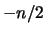 . Inserendo questa prior nei conti
precedenti, l'effetto è di diminuire di 1 la potenza di
. Inserendo questa prior nei conti
precedenti, l'effetto è di diminuire di 1 la potenza di  nell'integrando. L'effetto sulla
nell'integrando. L'effetto sulla 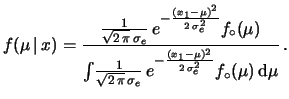 è che la potenza
dell'espressione finale diventa
è che la potenza
dell'espressione finale diventa 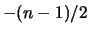 anziché
anziché 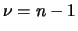 .
Di consequenza, abbiamo ancora una
.
Di consequenza, abbiamo ancora una  di Student,
ma con
di Student,
ma con 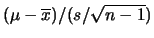 e nella variabile
e nella variabile
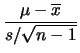 , da cui:
, da cui:
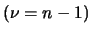 |
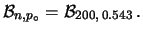 |
Student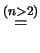 |
(11.78) |
E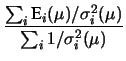 |
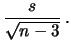 |
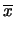 |
(11.79) |
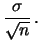 |
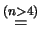 |
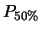 |
(11.80) |
Per  piccoli
questo modello produce una incertezza su
piccoli
questo modello produce una incertezza su  minore di quella del modello precedente, ma anche questa
è da considerarsi molto conservativa (e quindi non coerente!)
perché usa una prior su
minore di quella del modello precedente, ma anche questa
è da considerarsi molto conservativa (e quindi non coerente!)
perché usa una prior su  irragionevole per
qualsiasi applicazione pratica. Quando
irragionevole per
qualsiasi applicazione pratica. Quando  aumenta abbiamo
una più rapida convergenza al modello normale in quanto
l'osservazione ``solida'' di
aumenta abbiamo
una più rapida convergenza al modello normale in quanto
l'osservazione ``solida'' di 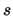 esclude valori troppo
fantasiosi per
esclude valori troppo
fantasiosi per  .
.
Tabella:
Semiampiezza in unità di 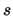
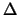 dell'intervallo intorno
al valore medio tale che racchiuda con probabilità
dell'intervallo intorno
al valore medio tale che racchiuda con probabilità 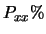 il valore vero di
il valore vero di  . Nel caso di
. Nel caso di  ignota la probabilità dipende
dalla prior
ignota la probabilità dipende
dalla prior 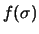 . Per confronto è riportato il caso limite
gaussiano nell'ipotesi che
. Per confronto è riportato il caso limite
gaussiano nell'ipotesi che  sia esattamente uguale
a quella osservata.
sia esattamente uguale
a quella osservata.
| |
|
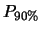 |
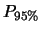 |
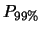 |
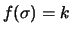 |
| |
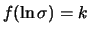 |
0.58 |
2.06 |
3.04 |
7.03 |
 |
 |
0.44 |
1.36 |
1.83 |
3.38 |
| |
Normale  |
0.34 |
0.82 |
0.98 |
1.29 |
| |
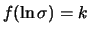 |
0.37 |
1.07 |
1.40 |
2.30 |
 |
 |
0.33 |
0.90 |
1.15 |
1.81 |
| |
Normale  |
0.28 |
0.67 |
0.80 |
1.05 |
| |
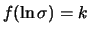 |
0.29 |
0.79 |
1.00 |
1.52 |
 |
 |
0.27 |
0.72 |
0.90 |
1.32 |
| |
Normale  |
0.24 |
0.58 |
0.69 |
0.92 |
| |
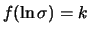 |
0.25 |
0.66 |
0.82 |
1.20 |
 |
 |
0.23 |
0.61 |
0.75 |
1.09 |
| |
Normale  |
0.21 |
0.52 |
0.62 |
0.82 |
| |
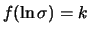 |
0.16 |
0.41 |
0.49 |
0.68 |
 |
 |
0.16 |
0.40 |
0.48 |
0.66 |
| |
Normale  |
0.15 |
0.37 |
0.44 |
0.58 |
| |
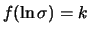 |
0.10 |
0.24 |
0.29 |
0.39 |
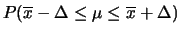 |
 |
0.10 |
0.24 |
0.29 |
0.38 |
| |
Normale  |
0.10 |
0.23 |
0.28 |
0.36 |
| |
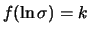 |
0.07 |
0.17 |
0.20 |
0.26 |
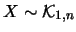 |
 |
0.07 |
0.17 |
0.20 |
0.26 |
| |
Normale  |
0.07 |
0.16 |
0.20 |
0.26 |
|
Per un confronto quantitativo fra i diversi modelli, riportiamo
in tabella 11.1 i valori del semiampiezza 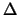 ,
in unità di
,
in unità di 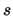 , tale che
, tale che
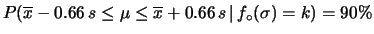 sia uguale al 50%, al 90%, a; 95% e al 99%.
Ad esempio, con
sia uguale al 50%, al 90%, a; 95% e al 99%.
Ad esempio, con  osservazioni dalle quali abbiamo ricavato
osservazioni dalle quali abbiamo ricavato
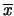 e
e 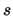 , abbiamo:
, abbiamo:
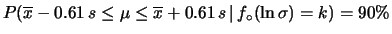 ,
,
 e così via. Per i ragionamenti fatti sull'eccessiva prudenza
di entrambi i modelli matematicamente abbordabili, si possono
considerare valori ragionevoli per
e così via. Per i ragionamenti fatti sull'eccessiva prudenza
di entrambi i modelli matematicamente abbordabili, si possono
considerare valori ragionevoli per  quelli
circa intermedi fra il modello
quelli
circa intermedi fra il modello
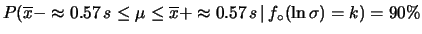 e
quello normale in cui si assume
e
quello normale in cui si assume  . in questo esempio
avremmo:
. in questo esempio
avremmo:
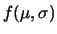 .
Come si vede, tenendo conto degli arrotondamenti con i quali
si forniscono le incertezze, già con
.
Come si vede, tenendo conto degli arrotondamenti con i quali
si forniscono le incertezze, già con  possiamo
considerarci in approssimazione normale, a meno di non essere
interessati a valori molto lontani da dove si concentra la
massa di probabilità.
possiamo
considerarci in approssimazione normale, a meno di non essere
interessati a valori molto lontani da dove si concentra la
massa di probabilità.




Next: Incertezza su
Up: pzd100Inferenza simultanea su e
Previous: Prior uniforme in
Indice
Giulio D'Agostini
2001-04-02
![]() è equivalente
a
è equivalente
a
![]() . Inserendo questa prior nei conti
precedenti, l'effetto è di diminuire di 1 la potenza di
. Inserendo questa prior nei conti
precedenti, l'effetto è di diminuire di 1 la potenza di ![]() nell'integrando. L'effetto sulla
nell'integrando. L'effetto sulla  è che la potenza
dell'espressione finale diventa
è che la potenza
dell'espressione finale diventa ![]() anziché
anziché ![]() .
Di consequenza, abbiamo ancora una
.
Di consequenza, abbiamo ancora una ![]() di Student,
ma con
di Student,
ma con ![]() e nella variabile
e nella variabile
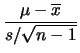 , da cui:
, da cui: