Prior uniforme in  :
:
in quanto l'integrale è pari a
 (la ben nota condizione di normalizzazine della gaussiana).
(la ben nota condizione di normalizzazine della gaussiana).
Figura:
Funzione densità di probabilità del
parametro  della gaussiana, in unità della deviazione standard sui valori
osservati, assumendo
della gaussiana, in unità della deviazione standard sui valori
osservati, assumendo
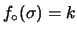 per
un numero
per
un numero  di osservazioni pari
3 (curva puntinata),
5 (tratteggiata) e 10 (continua).
di osservazioni pari
3 (curva puntinata),
5 (tratteggiata) e 10 (continua).
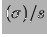 |
La forma della funzione è molto asimmetrica per  piccoli, mentre
tende ad una gaussiana per
piccoli, mentre
tende ad una gaussiana per
 . La figura
11.6
mostra degli esempi. Queste sono le espressioni di moda, valore
atteso e deviazione standard in unità di
. La figura
11.6
mostra degli esempi. Queste sono le espressioni di moda, valore
atteso e deviazione standard in unità di 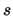
Moda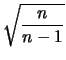 |
 |
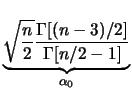 |
(11.82) |
E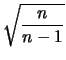 |
 |
![$\displaystyle \underbrace{\sqrt{\frac{n}{2}}
\frac{\Gamma[(n-3)/2]}{\Gamma[n/2-1]}}_{\alpha_0}$](img3443.png) |
(11.83) |
DevSt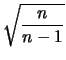 |
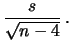 |
![$\displaystyle \frac{1}{\sqrt{2\,n}}
\underbrace{n\,\sqrt{\frac{2}{n-4}-
\frac{\Gamma^2\left[(n-3)/2\right]}
{\Gamma^2[n/2-1]}
}}_{\beta_0}$](img3444.png) |
(11.84) |
ove abbiamo designato con ``DevSt'' la deviazione standard di  , per
ovvi motivi. I due fattori complicati
, per
ovvi motivi. I due fattori complicati
 e
e
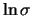 sono rilevanti soltanto per piccoli valori
sono rilevanti soltanto per piccoli valori  .
Per
.
Per
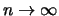 essi tendono a 1 e già per
essi tendono a 1 e già per
 differiscono dall'unità per meno del 50% (vedi figure
11.7 e 11.8).
differiscono dall'unità per meno del 50% (vedi figure
11.7 e 11.8).
Figura:
Fattore 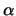 fra valore atteso di
fra valore atteso di  e deviazione standard delle osservazioni sperimentali in funzione
del numero di osservazioni. I rombi si riferiscono al caso
di prior uniforme in
e deviazione standard delle osservazioni sperimentali in funzione
del numero di osservazioni. I rombi si riferiscono al caso
di prior uniforme in  , le stelle al caso di uniforme in
, le stelle al caso di uniforme in  .
.
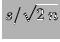 |
Figura:
Fattore 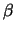 fra incertezza standard su
fra incertezza standard su  e
e
 in funzione
del numero di osservazioni. I rombi si riferiscono al caso
di prior uniforme in
in funzione
del numero di osservazioni. I rombi si riferiscono al caso
di prior uniforme in  , le stelle al caso di uniforme in
, le stelle al caso di uniforme in  .
.
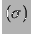 |
Quindi, per  grandi abbiamo i seguenti valori asintotici:
grandi abbiamo i seguenti valori asintotici:
E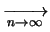 |
![$\displaystyle \xrightarrow[n\rightarrow\infty]{}$](img3452.png) |
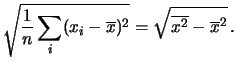 |
(11.85) |
DevSt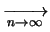 |
![$\displaystyle \xrightarrow[n\rightarrow\infty]{}$](img3452.png) |
 |
(11.86) |
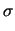 |
![$\displaystyle \xrightarrow[n\rightarrow\infty]{}$](img3452.png) |
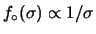 |
(11.87) |
(Si noti come il limite a normale è, per ora, una congettura basata
sull'osservazione delle curve. Nel paragrafo 11.7.4
vedremo un altro argomento più formale, basato
sulla distribuzione di probabilità di
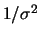 .)
.)
 (la ben nota condizione di normalizzazine della gaussiana).
(la ben nota condizione di normalizzazine della gaussiana).
![]() piccoli, mentre
tende ad una gaussiana per
piccoli, mentre
tende ad una gaussiana per
![]() . La figura
11.6
mostra degli esempi. Queste sono le espressioni di moda, valore
atteso e deviazione standard in unità di
. La figura
11.6
mostra degli esempi. Queste sono le espressioni di moda, valore
atteso e deviazione standard in unità di ![]()
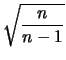
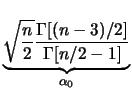
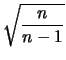
![$\displaystyle \underbrace{\sqrt{\frac{n}{2}}
\frac{\Gamma[(n-3)/2]}{\Gamma[n/2-1]}}_{\alpha_0}$](img3443.png)
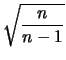
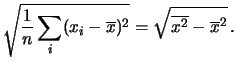
 : la prior
: la prior
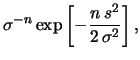 abbassa di un grado la potenza
di
abbassa di un grado la potenza
di 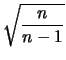
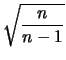
![$\displaystyle \underbrace{\sqrt{\frac{n}{2}}
\frac{\Gamma[(n/2-1]}{\Gamma[(n-1)/2]}}_{\alpha_1}$](img3457.png)
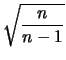
![$\displaystyle \frac{1}{\sqrt{2\,n}}
\underbrace{n\, \sqrt{\frac{2}{n-3}-
\frac{\Gamma^2\left[n/2-1\right]}
{\Gamma^2[(n-1)/2]}
}}_{\beta_1}$](img3458.png)
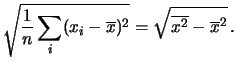
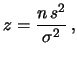 sono mostrate nelle figure 11.7 e
11.8.
sono mostrate nelle figure 11.7 e
11.8.