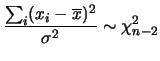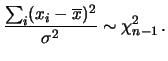Next: Conclusioni e raccomandazioni
Up: Caso di ignota
Previous: Incertezza su
Indice
Distribuzione di
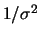
Abbiamo visto come, seppur con delle
scelte di convenienza formale delle prior,
le funzioni distribuzioni finali di  sono alquanto
inconsuete. È interessante studiare la forma di
sono alquanto
inconsuete. È interessante studiare la forma di
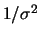 .
Chiamando
abbiamo dalle (11.81) e (11.88)
rispettivamente
.
Chiamando
abbiamo dalle (11.81) e (11.88)
rispettivamente
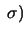 prior uniforme in prior uniforme in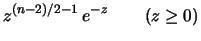 |
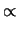 |
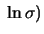 |
(11.95) |
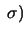 prior uniforme in prior uniforme in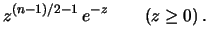 |
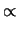 |
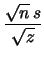 |
(11.96) |
Confrontando con la (8.43) si riconoscono nelle due funzioni
delle distribuzioni di 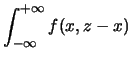 con un numero di gradi di libertà
rispettivamente
con un numero di gradi di libertà
rispettivamente 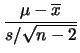 e
e 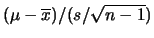 . Possiamo utilizzare questa
osservazione per ricavare in modo approssimato previsione e incertezza
di previsione di
. Possiamo utilizzare questa
osservazione per ricavare in modo approssimato previsione e incertezza
di previsione di  , sotto ipotesi che la linearizzazione
sia soddisfacente, ovvero l'incertezza relativa su
, sotto ipotesi che la linearizzazione
sia soddisfacente, ovvero l'incertezza relativa su 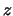 sia piccola,
ovvero ancora che
sia piccola,
ovvero ancora che  sia grande. Vediamo il solo caso di
prior uniforme in
sia grande. Vediamo il solo caso di
prior uniforme in
 , essendo l'altro caso simile e, comunque,
praticamente indistinguibile nei casi in cui vale la linearizzazione.
, essendo l'altro caso simile e, comunque,
praticamente indistinguibile nei casi in cui vale la linearizzazione.
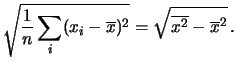 |
 |
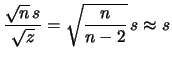 |
(11.97) |
E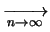 |
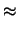 |
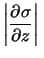 |
(11.98) |
DevSt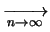 |
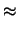 |
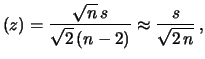 DevSt DevSt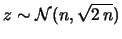 |
(11.99) |
riottendo i risultati asintotici calcolati direttamente.
In particolare, per
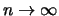 abbiamo che
abbiamo che
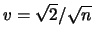 , con coefficiente di variazione
, con coefficiente di variazione
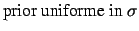 . Quindi la linearizzazione diventa una buona
approssimazione e anche
. Quindi la linearizzazione diventa una buona
approssimazione e anche 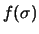 diventa gaussiana.
diventa gaussiana.
Terminiamo questo paragrafo facendo notare un altro modo di
scrivere il risultato ottenuto.




Next: Conclusioni e raccomandazioni
Up: Caso di ignota
Previous: Incertezza su
Indice
Giulio D'Agostini
2001-04-02
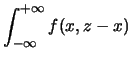 con un numero di gradi di libertà
rispettivamente
con un numero di gradi di libertà
rispettivamente 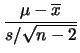 e
e  , essendo l'altro caso simile e, comunque,
praticamente indistinguibile nei casi in cui vale la linearizzazione.
, essendo l'altro caso simile e, comunque,
praticamente indistinguibile nei casi in cui vale la linearizzazione.
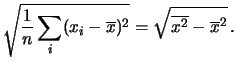
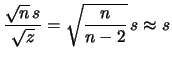
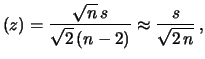 DevSt
DevSt