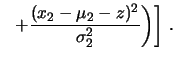Next: Caso di ignota
Up: Fattori di influenza non
Previous: Correzione per errori sistematici
Indice
Correlazione fra i risultati introdotta dalla non perfetta
conoscenza dello zero dello strumento
Un caso molto interessante è quando si misurano più grandezze
particolari con lo stesso strumento (o la stessa procedura) affetto
da incertezza di calibrazione. Facciamo di nuovo il semplice caso
di errore di zero non perfettamemente noto. Consideriamo
due valori veri 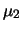 e
e 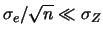 (l'estenzione a molti sarà immediata).
Indichiamo con
(l'estenzione a molti sarà immediata).
Indichiamo con 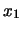 e
e 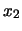 le due osservazioni
(o osservazioni equivalenti)e con
le due osservazioni
(o osservazioni equivalenti)e con
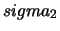 e
e 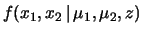 le deviazioni standard, per tener conto anche
di variazione della risposta del rivelatore (oppure di un diverso
numero di osservazioni individuali).
La verosimiglianza congiunta delle due osservazioni è data da
le deviazioni standard, per tener conto anche
di variazione della risposta del rivelatore (oppure di un diverso
numero di osservazioni individuali).
La verosimiglianza congiunta delle due osservazioni è data da
Applicando nuovamente le regole della probabilità abbiamo la seguente
inferenza congiunta su 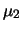 e
e 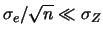 :
:
dove
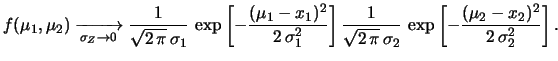 |
(11.44) |
Si riconosce una distribuzione normale bivariata che, nel
limite di 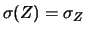 trascurabile si riduce a
trascurabile si riduce a
![$\displaystyle f(\mu_1,\mu_2) \xrightarrow[\sigma_Z\rightarrow 0]{} \frac{1}{\sq...
...2\,\pi}\,\sigma_2} \,\exp{\left[-\frac{(\mu_2-x_2)^2}{2\,\sigma_2^2}\right]}\,.$](img3346.png) |
(11.45) |
Se non c'è incertezza sulla costante di calibrazione i due risulatati
sono scorrelati e la funzione congiunta
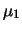 diventa uguale al prodotto di due gaussiane.
Nel caso generale, traiamo le seguenti conclusioni:
diventa uguale al prodotto di due gaussiane.
Nel caso generale, traiamo le seguenti conclusioni:




Next: Caso di ignota
Up: Fattori di influenza non
Previous: Correzione per errori sistematici
Indice
Giulio D'Agostini
2001-04-02
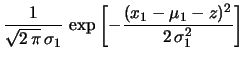
![$\displaystyle \frac{1}{\sqrt{2\,\pi}\,\sigma_1}
\,\exp{\left[-\frac{(x_1-\mu_1-z)^2}{2\,\sigma_1^2}\right]}$](img3337.png)
![$\displaystyle \times \,\frac{1}{\sqrt{2\,\pi}\,\sigma_2}
\,\exp\left[-\frac{(x_2-\mu_2-z)^2}{2\,\sigma_2^2}\right]$](img3338.png)
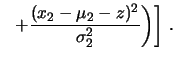
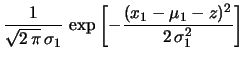
![$\displaystyle \frac{1}{\sqrt{2\,\pi}\,\sigma_1}
\,\exp{\left[-\frac{(x_1-\mu_1-z)^2}{2\,\sigma_1^2}\right]}$](img3337.png)
![$\displaystyle \times \,\frac{1}{\sqrt{2\,\pi}\,\sigma_2}
\,\exp\left[-\frac{(x_2-\mu_2-z)^2}{2\,\sigma_2^2}\right]$](img3338.png)