-
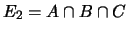 ;
;
-
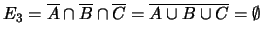 ;
;
-
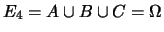 ;
;
-
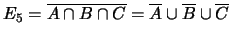 ;
;
-
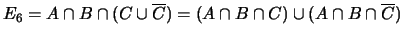 ;
;
-
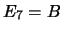 ,
ovvero
,
ovvero 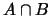 ;
;
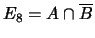 ;
;
-
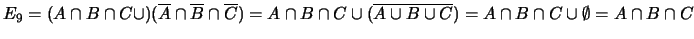 ;
;
-
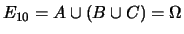 ;
;
-
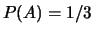 ;
;
-
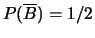 ;
;
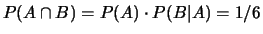 ;
;
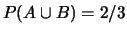 ;
;
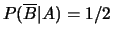 ;
;
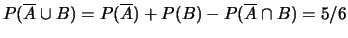 ;
;
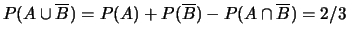 ;
;
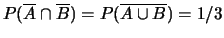 ;
;
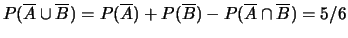 ;
;
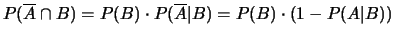 ;
;
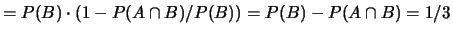
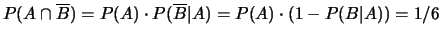 ;
;
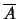 .
.
La seguente tabella aiuta a visualizzare le varie probabilità:

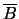

1/6 1/3 1/2 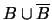
1/6 1/3 1/2 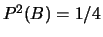
1/3 2/3 1
-
- Provarci...
-
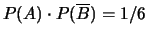 ;
;
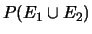 .
.
Naturalmente deve valere
Cosa ricordano le quattro espressioni trovate?
Il modo più semplice per capirlo è di pensare alla posizione dove si trova il proiettile dopo aver fatto ruotare il tamburo. Se si trova nella prima muore il primo, se nella seconda muore il secondo, e così via.
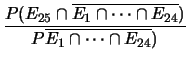 |
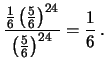 |
||
Probabilità che su 4 estrazioni, non capiti
un calzino dello stesso colore
del primo:
![]() . Quindi la probabilità
complementare è del
. Quindi la probabilità
complementare è del ![]() .
In questo caso si raggiunge la certezza
soltanto alla
.
In questo caso si raggiunge la certezza
soltanto alla ![]() estrazione (quando tutti gli altri calzini
sono estratti).
estrazione (quando tutti gli altri calzini
sono estratti).
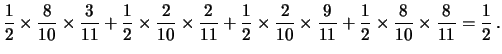 |
|||
conviene sempre cambiare. Se
Se si sapesse anche che il primo estratto era 58 ![]() (anche se il risultato è intuitivo, si raccomanda, per esercizio,
formalizzare la risposta anche in questo caso mediante
l'uso della formula di disintegrazione).
(anche se il risultato è intuitivo, si raccomanda, per esercizio,
formalizzare la risposta anche in questo caso mediante
l'uso della formula di disintegrazione).
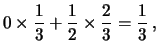 |
|||
da cui
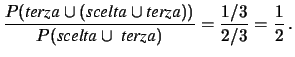 terza terza |
Nel secondo caso (intenzionalmente viene aperta una scatola vuota):
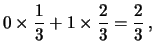 |
|||
dove