ne segue
Per la seconda domanda si utilizza la formula di Bayes:
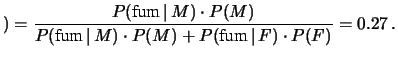 fum
fum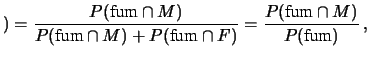
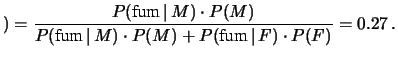 fum
fum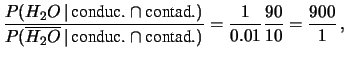 .
.
Ne segue:
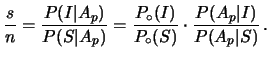 .
La maggior parte dei ``positivi'' sono sani.
.
La maggior parte dei ``positivi'' sono sani.
Come mai? Analizziamo il rapporto segnale/rumore:
Chiamando
Prendere un campione ``a rischio'' significa invece aumentare in
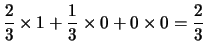 |
|||
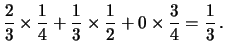 |
|||
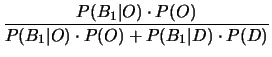 |
|||
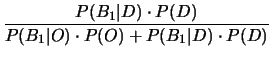 |
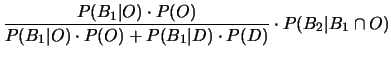 |
||
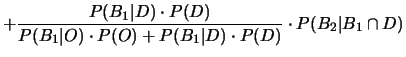 |
|||
Come ci si aspetta intuitivamente, è più alta la probabilità di ottenere una pallina nera, in quanto l'operazione più probabile è stata quella di estrarre una pallina bianca da dove ce ne sono 8 e metterla dove ce ne sono solo 2.
Succesivamente, indicando con
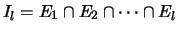 la
la 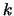 -ma estrazione, i cui esiti possono essere i
-ma estrazione, i cui esiti possono essere i 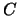 olori
olori
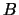 ianco o
ianco o 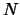 ero;
ero;
-
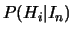 lo stato di informazione
dopo la
lo stato di informazione
dopo la  -ma estrazione,
-ma estrazione,
con
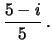 |
Dopo
Dopo
Dopo
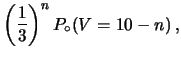 |
|||
dove
Probabilità iniziali:
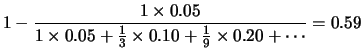 |
|||
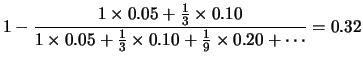 |
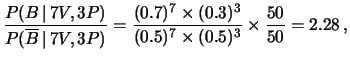 vale:
0.37, 0.46, 0.54, 0.62, 0.50, 0.58, 0.45, 0.54,
0.62, 0.69.
vale:
0.37, 0.46, 0.54, 0.62, 0.50, 0.58, 0.45, 0.54,
0.62, 0.69.
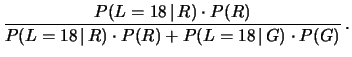 |
Poiché l'evento ``la temperatura assume un valore qualsiasi'' è un evento certo (
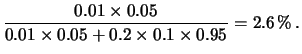 |
in quanto tutti gli altri termini sono nulli, o perché nulla la probabilità a priori della temperatura o perché nulla la probabilità condizionata di osservare una lettura di 18 da temperature superiori a 19
In conclusioni:
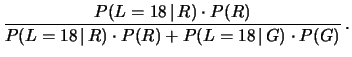 |
È interessante notare come il dubbio sul funzionamento del termometro cambi di nuovo i gradi di fiducia delle diverse temperature. Infatti nell'ipotesi che esso sia rotto la sua lettura non riaggiorna la probabilità iniziale. Riassumendo i risultati raggiunti nella seguente tabella abbiamo (con le probabilità in %):
| condizione | ||||
| 19 | 20 | 21 | 22 | |
| iniziale | 10 | 40 | 40 | 10 |
|
|
100 | 0 | 0 | 0 |
|
|
10 | 40 | 40 | 10 |
|
|
97.7 | 1.0 | 1.0 | 0.3 |
| condizione | ||||||
| 18 | 19 | 20 | 21 | 22 | 23 | |
| iniziale | 1 | 10 | 39 | 39 | 10 | 1 |
|
|
13.0 | 87.0 | 0 | 0 | 0 | 0 |
|
|
1 | 10 | 39 | 39 | 10 | 1 |
|
|
12.8 | 85.5 | 0.8 | 0.8 | 0.2 | 0.02 |
La madre del bambino può essere
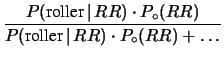 roller roller |
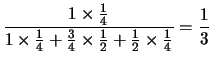 |
||
Ne segue una probabilità di
Delle 48 possibilità con cui la madre del bambino può ereditare i geni dei genitori ce ne sono 16 che danno luogo a (
Le probabilità iniziali dei geni della madre del bambino diventano ora:
Seguono:
Come ci si poteva attendere, sapere che la madre del bambino avesse un genitore roller aumenta le probabilità che anche lei lo fosse ( dall'
Il rifiuto a presentarsi manda definivamente a zero la probabilità,
se la commissione assume, ragionevolmente, che
![]() ``non si presenta''
``non si presenta''![]() ``imbroglione''
``imbroglione''![]() , mentre
, mentre
![]() ``non si presenta''
``non si presenta''![]() ``onesto''
``onesto''![]() .
.