



Next: Capitolo 7
Up: Soluzione dei problemi
Previous: Capitolo 5
Indice
- La variabile casuale può assumere con uguale
probabilità i valori
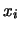 = -1, -2, -3,
2, 6, 10:
= -1, -2, -3,
2, 6, 10:
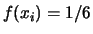 .
.
-
E
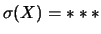 ,
,
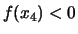 .
.
-
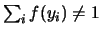 ;
;
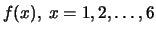 .
.
-
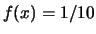 : {0.1, 0.2, 0.3, 0.3, 0.05, 0.05}.
Ne seguono i sette valori di probabilità richiesti:
0.2; 0; 0.6; 0.15; 0.6; 0.9; 0.6.
: {0.1, 0.2, 0.3, 0.3, 0.05, 0.05}.
Ne seguono i sette valori di probabilità richiesti:
0.2; 0; 0.6; 0.15; 0.6; 0.9; 0.6.
- Distribuzione discreta uniforme:
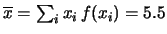 ;
;
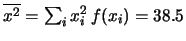 ;
;
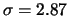 ;
;
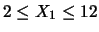 .
.
-
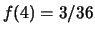 :
:
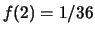 ,
,
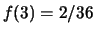 ,
,
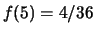 ,
,
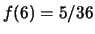 ,
,
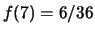 ,
,
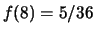 ,
,
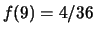 ,
,
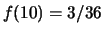 ,
,
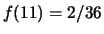 ,
,
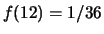 ,
,
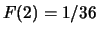 ;
;
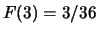 ,
,
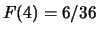 ,
,
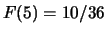 ,
,
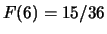 ,
,
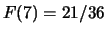 ,
,
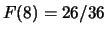 ,
,
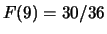 ,
,
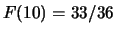 ,
,
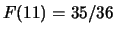 ,
,
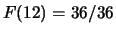 ,
,
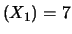 .
.
E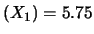 ,
Var
,
Var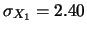 ;
;
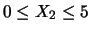
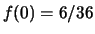 :
:
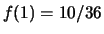 ,
,
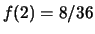 ,
,
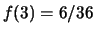 ,
,
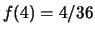 ,
,
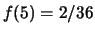 ,
,
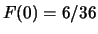 .
.
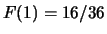 ,
,
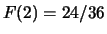 ,
,
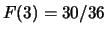 ,
,
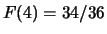 ,
,
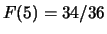 ,
,
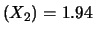 .
.
E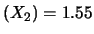 ,
Var
,
Var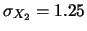 ,
,
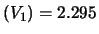 .
.
- La prima tensione può valere 2.25, 2.26, ...2.34 V
con distribuzione uniforme di probabilità. Analogalmente,
per la seconda si ha una distribuzione uniforme fra
2.05 e 2.14. Previsione e incertezza di previsione delle
due grandezza in Volt sono
rispettivamente16.1:
E
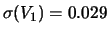 ,
,
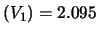 ;
E
;
E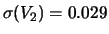 ,
,
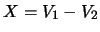 .
Costruendo una tabellina di tutte le possibilità,
in analogia con il caso
dei dadi di figura
6.2, si vede che la differenza
dei valori
.
Costruendo una tabellina di tutte le possibilità,
in analogia con il caso
dei dadi di figura
6.2, si vede che la differenza
dei valori 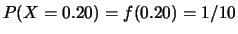 può assumere valori distanziati 0.01 V e
compresi fra 0.11 e 0.29 V, con probabilità
massima al centro
può assumere valori distanziati 0.01 V e
compresi fra 0.11 e 0.29 V, con probabilità
massima al centro
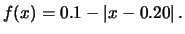 e decrescente verso il
valori estremi, rappresentabile matematicamente da:
Facendo i conti si ottiene che la differenza di tensione
ha una previsione
di 0.20 V con una incertezza di 0.04 V (si noti come l'incertezza sia
al di sotto della cifra meno significativa della lettura!)
e decrescente verso il
valori estremi, rappresentabile matematicamente da:
Facendo i conti si ottiene che la differenza di tensione
ha una previsione
di 0.20 V con una incertezza di 0.04 V (si noti come l'incertezza sia
al di sotto della cifra meno significativa della lettura!)
- Con i simboli precedentemente introdotti:
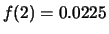 .
.
- La differenza di temperatura (in
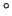 C)
è una variabile aleatoria
con distribuzione di probabilità:
C)
è una variabile aleatoria
con distribuzione di probabilità:
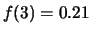 ,
,
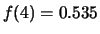 ,
,
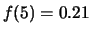 ,
,
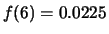 ,
,
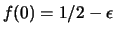 . Ne deriva un valore atteso
di 4.0
. Ne deriva un valore atteso
di 4.0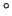 C, con incertezza standard di 0.8
C, con incertezza standard di 0.8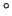 C.
C.
- 43.5, 64.3, 82.0, 94.3 e 99.7 %. Ovviamente la probabilità
che il numero si verifichi alla 101 estrazione
è sempre 1/18.
- Previsione 265720.5 giocate, con una incertezza uguale
alla previsione stessa.
- Chiamando
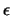 e
e 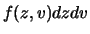 due numeri reali positivi e minori
di 1/2:
due numeri reali positivi e minori
di 1/2:
a) Se
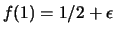 e
e
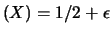 segue:
E
segue:
E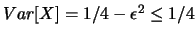 ,
,
![$ Var[X]=1/4-\epsilon^2 \le 1/4$](img4348.png) ;
;
b) Se
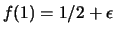 ,
,
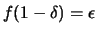 ,
,
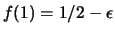 e
e
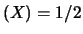 segue:
E
segue:
E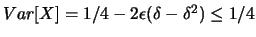 ,
,
![$ Var[X]=1/4-2\epsilon(\delta-\delta^2) \le 1/4$](img4353.png)
- No. Se
 e
e 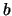 sono gli
estremi dell'intervallo, la deviazione standard
non può eccedere
sono gli
estremi dell'intervallo, la deviazione standard
non può eccedere
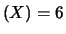 (vedi problema precedente).
(vedi problema precedente).
-
E
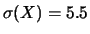 ,
,
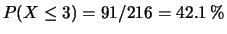 .
.
-
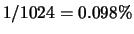 ;
in media deve attendere 6 turni prima di poter rientrare in gioco.
;
in media deve attendere 6 turni prima di poter rientrare in gioco.
-
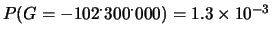 .
.
- Indicando con
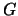 la vincita netta:
la vincita netta:
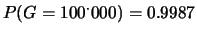 ;
;
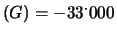 .
E
.
E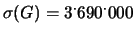 ;
;
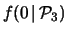 .
.
- Paradosso di San Pietroburgo.




Next: Capitolo 7
Up: Soluzione dei problemi
Previous: Capitolo 5
Indice
Giulio D'Agostini
2001-04-02