



Next: Numero di permutazioni di
Up: Disposizioni e combinazioni
Previous: Numero di -disposizioni di
Indice
Figura:
Numero di disposizioni semplici (senza ripetizione)
di tre oggetti presi due a due. Quelle cerchiate
corrispondono ad una scelta di disposizioni dalle quali le altre
differiscono per l'ordine degli oggetti (come indicato dalle frecce).
Il numero di disposizioni cerchiate corrisponde quindi al numeri di
combinazioni di  oggetti presi
oggetti presi  a
a  .
.
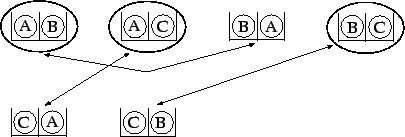 |
In alcuni problemi lo stesso oggetto non può essere messo
contemporaneamente in più caselle, come succede quando si pensa
a disposizioni di persone o di altri oggetti dei quali ne
esiste uno per tipo, oppure quando tale condizione è
richiesta nel problema.
Quindi si ha un primo vincolo dovuto al fatto che
il numero di caselle non può essere superiore al numero di oggetti:
Figura:
Come figura 3.1 per  e
e  .
.
 |
In questo caso si hanno  possibilità per la prima casella,
a ciascuna di queste possono essere associate
possibilità per la prima casella,
a ciascuna di queste possono essere associate
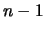 possibilità per la seconda e così via, fino a
possibilità per la seconda e così via, fino a 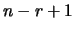 per la casella numero
per la casella numero  (vedi figura
3.1 per
(vedi figura
3.1 per  e
e  e
figura 3.2
per
e
figura 3.2
per  e
e  ).
).
Si è introdotto il simbolo 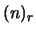 per indicare
il numero di
per indicare
il numero di  -disposizioni semplici
(o ``senza possibili ripetizioni'')
ed è stato moltiplicato numeratore e denominatore per
-disposizioni semplici
(o ``senza possibili ripetizioni'')
ed è stato moltiplicato numeratore e denominatore per 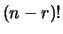 per
semplificare il calcolo. Per riottenere la
(3.3) dalla (3.4)
anche nel caso
per
semplificare il calcolo. Per riottenere la
(3.3) dalla (3.4)
anche nel caso  (ovvero
(ovvero 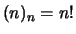 )
si adotta la convenzione
Per i problemi del punto 2 otteniamo:
)
si adotta la convenzione
Per i problemi del punto 2 otteniamo:
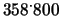 parole e
parole e
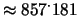 miliardi di squadre.
miliardi di squadre.
È da notare come anche l'operazione elementare di conteggio possa
essere considerata come una  -disposizione con
-disposizione con  .
.




Next: Numero di permutazioni di
Up: Disposizioni e combinazioni
Previous: Numero di -disposizioni di
Indice
Giulio D'Agostini
2001-04-02
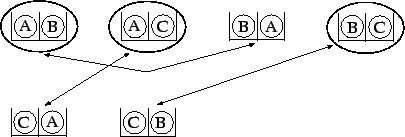
![]() possibilità per la prima casella,
a ciascuna di queste possono essere associate
possibilità per la prima casella,
a ciascuna di queste possono essere associate
![]() possibilità per la seconda e così via, fino a
possibilità per la seconda e così via, fino a ![]() per la casella numero
per la casella numero ![]() (vedi figura
3.1 per
(vedi figura
3.1 per ![]() e
e ![]() e
figura 3.2
per
e
figura 3.2
per ![]() e
e ![]() ).
).
![]() -disposizione con
-disposizione con ![]() .
.