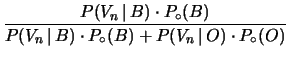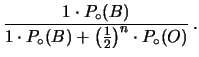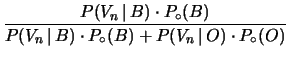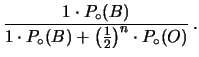Next: Confronto fra inferenza diretta
Up: Il caso del sospetto
Previous: I ``fatti''
Indice
Le ipotesi a cui siamo interessati sono quelle della partizione
dell'evento certo
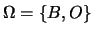 , ovvero
dalle ipotesi che l'amico sia Baro o Onesto. Indichiamo
con
, ovvero
dalle ipotesi che l'amico sia Baro o Onesto. Indichiamo
con 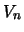 l'evento ``vince
l'evento ``vince  volte consecutive''. Supponiamo,
per semplificare i conti, che
se l'amico è baro vinca sempre (
volte consecutive''. Supponiamo,
per semplificare i conti, che
se l'amico è baro vinca sempre (
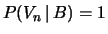 ), mentre
se è onesto vinca secondo le leggi della probabilità,
ossia
), mentre
se è onesto vinca secondo le leggi della probabilità,
ossia
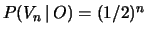 .
Applicando la formula di Bayes otteniamo la probabilità
dell'ipotesi Baro subordinata alle
.
Applicando la formula di Bayes otteniamo la probabilità
dell'ipotesi Baro subordinata alle  vincite:
vincite:
Rimane da assegnare la probabilità iniziale
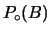 .
Chiaramente un estraneo che ci invitasse a giocare d'azzardo
si renderebbe immediatamente sospetti e la probabilità
iniziale sarebbe ritenuta
prossima a 1. Volendo essere generosi,
in quanto si tratta pur sempre di un vecchio amico,
fissiamo un valore basso, pari al
.
Chiaramente un estraneo che ci invitasse a giocare d'azzardo
si renderebbe immediatamente sospetti e la probabilità
iniziale sarebbe ritenuta
prossima a 1. Volendo essere generosi,
in quanto si tratta pur sempre di un vecchio amico,
fissiamo un valore basso, pari al 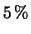 :
:
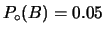 ,
,
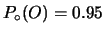 .
.
La seguente tabella riporta i valori
della probabilità in funzione del numero di vittorie consecutive:
 |
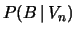 |
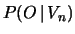 |
| |
(%) |
(%) |
| 0 |
5.0 |
95.0 |
| 1 |
9.5 |
90.5 |
| 2 |
17.4 |
82.6 |
| 3 |
29.4 |
70.6 |
| 4 |
45.7 |
54.3 |
| 5 |
62.7 |
37.3 |
| 6 |
77.1 |
22.9 |
| ... |
... |
... |
Come naturale, all'aumentare del numero di vittorie consecutive,
cresce il sospetto che il vecchio amico stia imbrogliando.




Next: Confronto fra inferenza diretta
Up: Il caso del sospetto
Previous: I ``fatti''
Indice
Giulio D'Agostini
2001-04-02