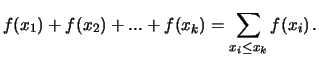Next: Distribuzioni elementari notevoli
Up: Variabili casuali e distribuzioni
Previous: Esempi di costruzione di
Indice
Proprietà delle distribuzioni di
probabilità discrete
La funzione di probabilità 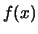 , avendo il significato di probabilità
di eventi di una classe completa,
deve soddisfare le seguenti condizioni:
, avendo il significato di probabilità
di eventi di una classe completa,
deve soddisfare le seguenti condizioni:
(Si faccia attenzione all'uso flessibile
degli indici. A volte, per alleggerire
la notazione verranno omessi. Altre volte, quando la variabile  può assumere valori che differiscono fra loro di una unità,
verrà utilizzato lo stesso simbolo
può assumere valori che differiscono fra loro di una unità,
verrà utilizzato lo stesso simbolo  come indice delle sommatorie.
Inoltre, gli estremi delle sommatorie sono spesso omessi per indicare
che, implicitamente, sono considerati tutti i valori possibili.
Ad esempio, la 3) potrebbe essere scritta più
sinteticamente come
come indice delle sommatorie.
Inoltre, gli estremi delle sommatorie sono spesso omessi per indicare
che, implicitamente, sono considerati tutti i valori possibili.
Ad esempio, la 3) potrebbe essere scritta più
sinteticamente come
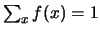 .)
.)
La proprietà 2) deriva dal fatto che valori diversi della realizzazione
di una variabile casuale sono incompatibili.
La condizione 3) è anche chiamata condizione di normalizzazione
(si dice che ``la distribuzione di probabilità
è normalizzata ad 1'').
La somma è da intendersi estesa a tutti i possibili valori che
può assumere  .
.
In alcuni casi può avere interesse trovare la probabilità che la
variabile casuale  assuma un valore uguale o minore di un certo
assuma un valore uguale o minore di un certo
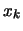 . Si introduce allora il concetto di
probabilità cumulativa, descritta dalla funzione di
ripartizione
. Si introduce allora il concetto di
probabilità cumulativa, descritta dalla funzione di
ripartizione 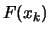 :
:
È comodo poter estendere la somma a tutti i valori reali
di  , sottintendendo che,
al di fuori del campo di definizione di
, sottintendendo che,
al di fuori del campo di definizione di 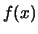 ,
,
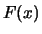 è pari al valore che essa assume per
è pari al valore che essa assume per 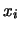 immediatamente inferiore
ad
immediatamente inferiore
ad  e
per il quale la
e
per il quale la 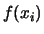 sia definita6.6.
sia definita6.6.
La funzione di ripartizione gode delle seguenti proprietà
che discendono direttamente dalla definizione:
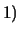 |
|
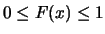 |
(6.7) |
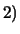 |
|
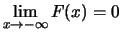 |
(6.8) |
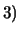 |
|
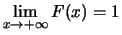 |
(6.9) |
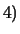 |
|
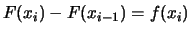 |
(6.10) |
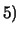 |
|
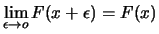 continuità a destra continuità a destra |
(6.11) |
La Fig. 6.3 mostra anche le funzioni di ripartizione delle
variabili  e
e 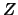 definite nel paragrafo precedente.
definite nel paragrafo precedente.




Next: Distribuzioni elementari notevoli
Up: Variabili casuali e distribuzioni
Previous: Esempi di costruzione di
Indice
Giulio D'Agostini
2001-04-02
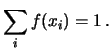
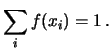
![]() .
.
![]() assuma un valore uguale o minore di un certo
assuma un valore uguale o minore di un certo
![]() . Si introduce allora il concetto di
probabilità cumulativa, descritta dalla funzione di
ripartizione
. Si introduce allora il concetto di
probabilità cumulativa, descritta dalla funzione di
ripartizione ![]() :
: