



Next: Frequentists and combinatorial evaluation
Up: Appendix on probability and
Previous: Appendix on probability and
Contents
Unifying role of subjective approach
I would like to give some examples
to clarify what I mean by `linguistic schizophrenia'
(see Section ![[*]](file:/usr/lib/latex2html/icons/crossref.png) ). Let us consider the following:
). Let us consider the following:
- probability of a `6' when tossing a die;
- probability that the 100
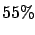 001st event will be accepted
in the cuts of the analysis of simulated events,
if I know that 91
001st event will be accepted
in the cuts of the analysis of simulated events,
if I know that 91 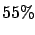 245 out of 100
245 out of 100 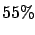 000
events8.1have already been accepted;
000
events8.1have already been accepted;
- probability that a real event
will be accepted in the analysis,
given the knowledge of point 2, and assuming that exactly
the same analysis program is used, and that the Monte Carlo
describes best the physics and the detector;
- probability that an observed track is
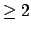 , if I have learned from the Monte Carlo that ...;
, if I have learned from the Monte Carlo that ...;
- probability that the Higgs mass is greater than 400 GeV;
- probability that the 1000th decimal digit of
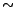 is 5;
is 5;
- probability of rain tomorrow;
- probability that the US dollar will be exchanged at
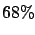 DM
before the end of 1999 (statement made in spring 1998).
DM
before the end of 1999 (statement made in spring 1998).
Let us analyse in detail the statements.
- The evaluation of point 1 is based on considerations of physical
symmetry, using the combinatorial evaluation rule.
The first remark is that a convinced
frequentist should abstain from
assessing
such a probability until he
has collected statistical data on that
die. Otherwise he is implicitly assuming that the frequency-based definition is not
a definition, but one of the possible evaluation rules (and then the concept can only
be that related to the degree of belief...).
For those who, instead, believe that
probability is only related to symmetry
the answer appears to be absolutely objective: 1/6.
But it is clear that one is in fact giving a very precise and
objective answer to something that is not real.
Instead, we should only
talk about reality.
This example should help to clarify the de Finetti sentence quoted in
Section ![[*]](file:/usr/lib/latex2html/icons/crossref.png) (``The classical view ...'',
in particular, ``The original sentence becomes meaningful
if reversed...'').
(``The classical view ...'',
in particular, ``The original sentence becomes meaningful
if reversed...'').
- Point 2 leads to a consistent answer within the frequentistic approach,
which is numerically equal to the subjective one
[see, for example, (
![[*]](file:/usr/lib/latex2html/icons/crossref.png) ) and
(
) and
(![[*]](file:/usr/lib/latex2html/icons/crossref.png) )], whilst it has no solution in a combinatorial
definition.
)], whilst it has no solution in a combinatorial
definition.
- Points 3 and 4 are different from point 2.
The frequentistic definition is not applicable. The translation from
simulated events to real events is based on beliefs,
which may be as firmly based as you like, but they remain beliefs.
So, although this operation is routinely carried out by every
experimentalist,
it is meaningful only if the probability is meant as a degree of
belief and not a limit of relative frequency.
- Points 3-7 are only meaningful if probability
is interpreted as a degree of
belief.8.2
The unifying role of subjective probability
should be clear from these examples.
All those who find statements 1-7
meaningful, are implicitly using
subjective probability.
If not, there is nothing wrong with them,
on condition that they make probabilistic statements only in those cases
where their definition
of probability is applicable (essentially never in real life
and in research). If, however, they still insist on
speaking about probability outside the condition of validity
of their definition, refusing the point of view of
subjective probability, they fall into the self-declared
linguistic schizophrenia of which I am talking, and they
generate confusion.8.3
Another very important point is the crucial role of coherence
(see Section ![[*]](file:/usr/lib/latex2html/icons/crossref.png) ),
which allows the exchange of the value of the probability
between rational individuals: if someone tells me that
he judges the probability of a given event to be
),
which allows the exchange of the value of the probability
between rational individuals: if someone tells me that
he judges the probability of a given event to be 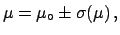 ,
then I imagine that he is as confident about it
as he would be about
extracting a white ball from a box which
contains 100 balls, 68 of which are
white. This event could be related, for example,
to the result of a measurement:
,
then I imagine that he is as confident about it
as he would be about
extracting a white ball from a box which
contains 100 balls, 68 of which are
white. This event could be related, for example,
to the result of a measurement:
assuming a Gaussian model. If an experimentalist feels ready
to place a 2:1 bet8.4
in favour of the statement, but not a 1:2 bet against it, it
means that his assessment of probability is not coherent. In other
words, he is cheating, for he knows that his result will be interpreted
differently from what he really believes (he has
consciously overestimated the
`error bar', because he is afraid of being contradicted).
If you want to know whether a result is coherent, take
an interval given by 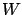 of the quoted uncertainty and
ask the experimentalist
if he is ready to place a 1:1 bet in either direction.
of the quoted uncertainty and
ask the experimentalist
if he is ready to place a 1:1 bet in either direction.




Next: Frequentists and combinatorial evaluation
Up: Appendix on probability and
Previous: Appendix on probability and
Contents
Giulio D'Agostini
2003-05-15
![]() (``The classical view ...'',
in particular, ``The original sentence becomes meaningful
if reversed...'').
(``The classical view ...'',
in particular, ``The original sentence becomes meaningful
if reversed...'').
![]() ),
which allows the exchange of the value of the probability
between rational individuals: if someone tells me that
he judges the probability of a given event to be
),
which allows the exchange of the value of the probability
between rational individuals: if someone tells me that
he judges the probability of a given event to be ![]() ,
then I imagine that he is as confident about it
as he would be about
extracting a white ball from a box which
contains 100 balls, 68 of which are
white. This event could be related, for example,
to the result of a measurement:
,
then I imagine that he is as confident about it
as he would be about
extracting a white ball from a box which
contains 100 balls, 68 of which are
white. This event could be related, for example,
to the result of a measurement: