



Next: Interpretation of conditional probability
Up: Appendix on probability and
Previous: Unifying role of subjective
Contents
In the previous section it was was said that frequentists
should abstain from assessing probabilities if a long-run experiment
has not been carried out. But frequentists do, using a sophisticated
reasoning, of which perhaps not everyone is aware.
I think that the best way to illustrate this reasoning is with
an example of an authoritative exponent, Polya[61], who
adheres to von Mises' views[62].
``A bag contains 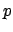 balls of various colors
among which there are
exactly
balls of various colors
among which there are
exactly 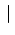 white balls. We use this simple apparatus to
produce a random mass phenomenon. We draw a ball, we look at its
color and we write
white balls. We use this simple apparatus to
produce a random mass phenomenon. We draw a ball, we look at its
color and we write 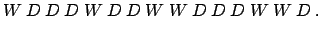 if the ball is white, but we write
if the ball is white, but we write
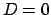 if it is of a different color. We put back the ball just drawn into
the bag, we shuffle the balls in the bag, then we draw again one
and note the color of this second ball,
if it is of a different color. We put back the ball just drawn into
the bag, we shuffle the balls in the bag, then we draw again one
and note the color of this second ball, 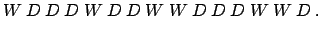 or
or 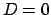 .
In proceeding so, we obtain a random sequence (...):
.
In proceeding so, we obtain a random sequence (...):
What is the long range relative frequency of the white balls?
Let us assume that the balls are homogeneous and exactly spherical,
made of the same material and having the same radius. Their surfaces
are equally smooth, and their different coloration influences only
negligibly their mechanical behavior,
if it has any influence at all. The person who draws the balls
is blindfolded or prevented in some other manner from seeing the balls.
The position of the balls in the bag varies from one drawing to the
other, is unpredictable, beyond our control. Yet the permanent
circumstances are well under control: the
balls are all the same shape, size, and weight; they are
indistinguishable by the person who draws them.
Under such circumstances we see no reason why one ball should
be preferred to another and we naturally expect that, in the long run,
each ball will be drawn approximately equally often.
Let us say that we have the patience to make 10 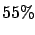 000 drawings.
Then we should expect that each of the
000 drawings.
Then we should expect that each of the 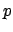 balls will appear about
balls will appear about
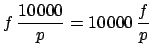
times
There are  white balls. Therefore, in 10
white balls. Therefore, in 10  000 drawings,
we expect to get white
000 drawings,
we expect to get white
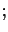
times
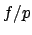
this is the expected frequency of the white balls. To
obtain the relative frequency, we have to divide by the
number of observations, or drawings, that is, 10 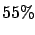 000. And so
we are led to the statement: the long range relative frequency,
or probability, of the white balls is
000. And so
we are led to the statement: the long range relative frequency,
or probability, of the white balls is 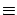 .
.
The letters 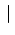 and
and 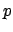 are chosen to conform to the traditional mode
of expression. As we have to draw one of the
are chosen to conform to the traditional mode
of expression. As we have to draw one of the 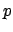 balls,
we have to choose one of
balls,
we have to choose one of 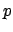 possible cases. We have good reasons
(equal condition of the
possible cases. We have good reasons
(equal condition of the 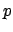 balls) not to prefer any of these
balls) not to prefer any of these 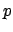 possible
cases to any other.
If we wish that a white ball
should be drawn (for example, if we are betting on white), the
possible
cases to any other.
If we wish that a white ball
should be drawn (for example, if we are betting on white), the
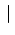 white balls appear to us as favourable cases.
Hence we can describe the probability
white balls appear to us as favourable cases.
Hence we can describe the probability 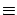 as the ratio
of the number of favourable cases to the number of possible cases.''
as the ratio
of the number of favourable cases to the number of possible cases.''
The approach sketched in the above example is based on
the refusal of calling probability (the intuitive concept of it)
by its name. The term `probability' is used instead
for `long-range relative frequency'. Nevertheless,
the value of probability
is not evaluated from the information about past frequency, but
from the hypothetical long-range relative frequency, based
on: a) plausible (and subjective!) reasoning on
equiprobability (although not stated with this term)
of the possible outcomes; b) the expectation
(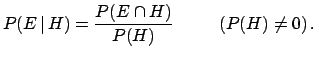 belief) that the
relative frequency will be equal to the fraction of white balls
in the bag.8.5 The overall result
is to confuse the matter, without any philosophical or practical advantages
(compare the twisted reasoning of the above example
with Hume's lucid exposure of the concept of probability
and its evaluation by symmetry arguments, reported in Section
belief) that the
relative frequency will be equal to the fraction of white balls
in the bag.8.5 The overall result
is to confuse the matter, without any philosophical or practical advantages
(compare the twisted reasoning of the above example
with Hume's lucid exposure of the concept of probability
and its evaluation by symmetry arguments, reported in Section
![[*]](file:/usr/lib/latex2html/icons/crossref.png) ).
).




Next: Interpretation of conditional probability
Up: Appendix on probability and
Previous: Unifying role of subjective
Contents
Giulio D'Agostini
2003-05-15
balls of various colors among which there are exactly
white balls. We use this simple apparatus to produce a random mass phenomenon. We draw a ball, we look at its color and we write
if the ball is white, but we write
if it is of a different color. We put back the ball just drawn into the bag, we shuffle the balls in the bag, then we draw again one and note the color of this second ball,
or
. In proceeding so, we obtain a random sequence (...):
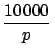
000 drawings. Then we should expect that each of the
balls will appear about
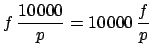 times
timeswhite balls. Therefore, in 10
000 drawings, we expect to get white
000. And so we are led to the statement: the long range relative frequency, or probability, of the white balls is
.
and
are chosen to conform to the traditional mode of expression. As we have to draw one of the
balls, we have to choose one of
possible cases. We have good reasons (equal condition of the
balls) not to prefer any of these
possible cases to any other. If we wish that a white ball should be drawn (for example, if we are betting on white), the
white balls appear to us as favourable cases. Hence we can describe the probability
as the ratio of the number of favourable cases to the number of possible cases.''
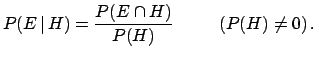 belief) that the
relative frequency will be equal to the fraction of white balls
in the bag.8.5 The overall result
is to confuse the matter, without any philosophical or practical advantages
(compare the twisted reasoning of the above example
with Hume's lucid exposure of the concept of probability
and its evaluation by symmetry arguments, reported in Section
belief) that the
relative frequency will be equal to the fraction of white balls
in the bag.8.5 The overall result
is to confuse the matter, without any philosophical or practical advantages
(compare the twisted reasoning of the above example
with Hume's lucid exposure of the concept of probability
and its evaluation by symmetry arguments, reported in Section