Subjective definition of probability

Figure: Certain and uncertain events[28].

So, ``what is probability?'' Consulting a good dictionary helps. Webster's states, for example, that ``probability is the quality, state, or degree of being probable'', and then that probable means ``supported by evidence strong enough to make it likely though not certain to be true''. The concept of probable arises in reasoning when the concept of certain is not applicable. When it is impossible to state firmly if an event (we use this word as a synonym for any possible statement, or proposition, relative to past, present or future) is true or false, we just say that this is possible, probable. Different events may have different levels of probability, depending whether we think that they are more likely to be true or false (see Figure ). The concept of probability is then simply

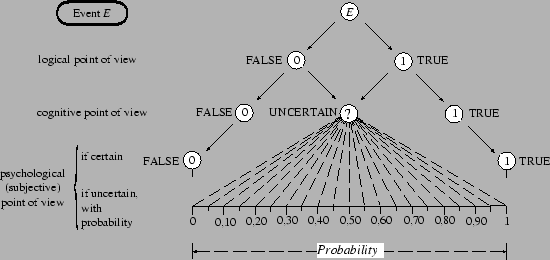
a measure of the degree of belief that an event will^3.2 occur.

This is the kind of definition that one finds in Bayesian books[11,19,29,30,31] and the formulation cited here is that given in the ISO Guide[3], of which we will talk later.

At first sight this definition does not seem to be superior to the combinatorial or the frequentistic ones. At least they give some practical rules to calculate ``something''. Defining probability as ``degree of belief'' seems too vague to be of any use. We need, then, some explanation of its meaning; a tool to evaluate it - and we will look at this tool (Bayes' theorem) later. We will end this section with some explanatory remarks on the definition, but first let us discuss the advantages of this definition.

• It is natural, very general and can be applied to any thinkable event, independently of the feasibility of making an inventory of all (equally) possible and favourable cases, or of repeating the experiment under conditions of equal probability.
• It avoids the linguistic schizophrenia of having to distinguish ``scientific'' probability from ``non scientific'' probability used in everyday reasoning (though a meteorologist might feel offended to hear that evaluating the probability of rain tomorrow is ``not scientific'').
• As far as measurements are concerned, it allows us to talk about the probability of the true value of a physical quantity, or of any scientific hypothesis. In the frequentistic frame it is only possible to talk about the probability of the outcome of an experiment, as the true value is considered to be a constant. This approach is so unnatural that most physicists speak of ``$95\, \%$ probability that the mass of the top quark is between $\ldots$'', although they believe that the correct definition of probability is the limit of the frequency.
• It is possible to make a very general theory of uncertainty which can take into account any source of statistical or systematic error, independently of their distribution.

To get a better understanding of the subjective definition of probability let us take a look at odds in betting. The higher the degree of belief that an event will occur, the higher the amount of money $A$ that someone (``a rational better'') is ready to pay in order to receive a sum of money $B$ if the event occurs. Clearly the bet must be acceptable in both directions (``coherent'' is the correct adjective), i.e. the amount of money $A$ must be smaller or equal to $B$ and not negative (who would accept such a bet?). The cases of $A=0$ and $A=B$ mean that the events are considered to be false or true, respectively, and obviously it is not worth betting on certainty. They are just limit cases, and in fact they can be treated with standard logic. It seems reasonable^3.3 that the amount of money $A$ that one is willing to pay grows linearly with the degree of belief. It follows that if someone thinks that the probability of the event $E$ is $p$, then he will bet $A=p\,B$ to get $B$ if the event occurs, and to lose $p\,B$ if it does not. It is easy to demonstrate that the condition of ``coherence'' implies that $0\le p\le 1$.

What has gambling to do with physics? The definition of probability through betting odds has to be considered operational, although there is no need to make a bet (with whom?) each time one presents a result. It has the important role of forcing one to make an honest assessment of the value of probability that one believes. One could replace money with other forms of gratification or penalization, like the increase or the loss of scientific reputation. Moreover, the fact that this operational procedure is not to be taken literally should not be surprising. Many physical quantities are defined in a similar way. Think, for example, of the textbook definition of the electric field, and try to use it to measure $\vec{E}$ in the proximity of an electron. A nice example comes from the definition of a poisonous chemical compound: it would be lethal if ingested. Clearly it is preferable to keep this operational definition at a hypothetical level, even though it is the best definition of the concept.