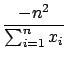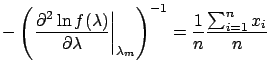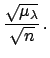Next: Combination of results: general
Up: Poisson model: dependence on
Previous: Dependence on priors
Contents
Results may be combined in a natural way
making an interactive use of
Bayesian inference.
As a first case we assume
several experiments having the same efficiency and exposure time.
- Prior knowledge:
- Experiment 1 provides Data
 :
:
- Experiment 2 provides Data
 :
:
- Combining
 similar independent experiments we get
similar independent experiments we get
Then it is possible to evaluate expected value, standard deviation,
and probability intervals.
As an exercise, let us analyse the two extreme cases, starting
from a uniform prior:
-
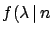
- if none of the
 similar
experiments has observed events
we have
similar
experiments has observed events
we have
 expts expts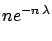 evts evts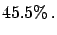 |
 |
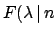 |
|
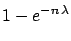 expts expts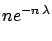 evts evts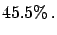 |
 |
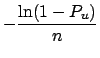 |
|
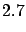 |
 |
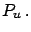 with probability with probability 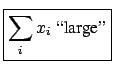 |
|
-
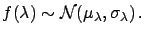
- If the number of observed events is large (and the prior flat),
the result will be normally distributed:
Then, in this case it is more practical to use maximum likelihood
methods than to make integrals (see Section
![[*]](file:/usr/lib/latex2html/icons/crossref.png) ).
From the maximum of
).
From the maximum of
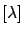 , in correspondence of
, in correspondence of
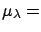 ,
we easily get:
,
we easily get:
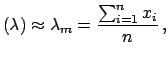
E
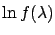
and from the second derivative of
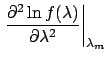 around the maximum:
around the maximum:




Next: Combination of results: general
Up: Poisson model: dependence on
Previous: Dependence on priors
Contents
Giulio D'Agostini
2003-05-15
 :
:




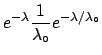
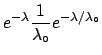
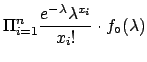
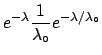
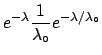
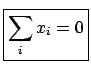
 :
:




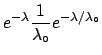
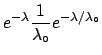
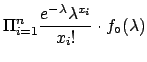
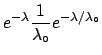
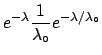
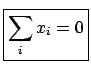
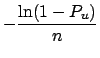
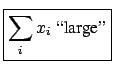
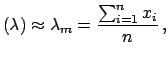 E
E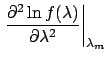 around the maximum:
around the maximum: