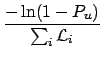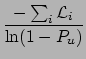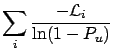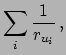Next: Including systematic effects
Up: Poisson model: dependence on
Previous: Combination of results from
Contents
Combination of results: general case
The previous case is rather artificial and can be used, at most,
to combine several measurements of the same experiment repeated
 times, each with the same running time. In general,
experiments differ in size, efficiency, and
running time. A result on
times, each with the same running time. In general,
experiments differ in size, efficiency, and
running time. A result on  is no
longer meaningful.
The quantity which is independent from these contingent
factors is the rate, related to
is no
longer meaningful.
The quantity which is independent from these contingent
factors is the rate, related to  by
where
by
where 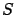 indicates the efficiency,
indicates the efficiency, 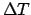 the generic `size'
(either area or volume, depending on whatever is relevant for the
kind of detection) and
the generic `size'
(either area or volume, depending on whatever is relevant for the
kind of detection) and 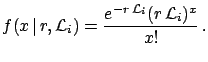 the running time: all the
factors have been grouped into a generic `integrated luminosity'
the running time: all the
factors have been grouped into a generic `integrated luminosity' 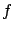 which quantify the effective exposure of the experiment.
which quantify the effective exposure of the experiment.
As seen in the previous case, the combined result can be achieved
using Bayes' theorem iteratively, but now one has to pay attention
to the fact that:
- the observable is Poisson distributed, and the each experiment
can infer a
 parameter;
parameter;
- the result on
 must be translated9.2into a result on
must be translated9.2into a result on 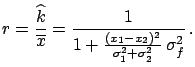 .
.
Starting from a prior on 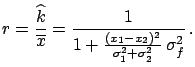 (e.g. a monopole flux) and
going from experiment 1 to
(e.g. a monopole flux) and
going from experiment 1 to  we have
we have
- from
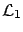 and
and
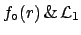 we get
we get
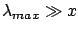 ;
then, from the data we perform the inference on
;
then, from the data we perform the inference on  and then on
and then on 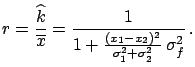 :
:
- The process is iterated for the second experiment:
- and so on for all the experiments.
Lets us see in detail the case of null
observation in all experiments
(
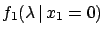 ) ,
starting from a uniform distribution.
) ,
starting from a uniform distribution.
- Experiment 1:
-
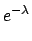 |
 |
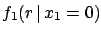 |
|
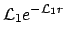 |
 |
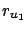 |
(9.7) |
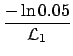 |
 |
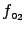 at 95% probability at 95% probability |
(9.8) |
- Experiment 2:
-
- Experiment
 :
:
-
 |
(9.9) |
The final result is insensitive to the data grouping.
As the intuition suggests, many experiments give the
same result of a single experiment with equivalent luminosity.
To get the upper limit, we calculate, as usual, the cumulative
distribution and require a certain probability 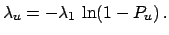 for
for 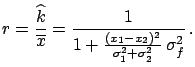 to be below
to be below
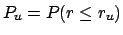 [i.e.
[i.e.
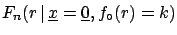 ]:
]:
obtaining the following rule for the combination of
upper limits on rates:
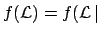 |
(9.10) |
We have considered here only the case in which no background is
expected, but it is not difficult to take background into account,
following what has been said in Section ![[*]](file:/usr/lib/latex2html/icons/crossref.png) .
.




Next: Including systematic effects
Up: Poisson model: dependence on
Previous: Combination of results from
Contents
Giulio D'Agostini
2003-05-15
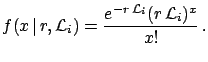 the running time: all the
factors have been grouped into a generic `integrated luminosity'
the running time: all the
factors have been grouped into a generic `integrated luminosity' 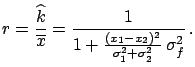 .
.
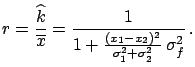 (e.g. a monopole flux) and
going from experiment 1 to
(e.g. a monopole flux) and
going from experiment 1 to 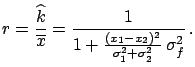 :
:
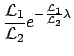
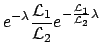
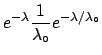
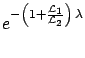
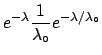
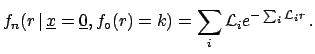
 to be below
to be below