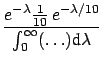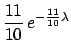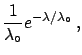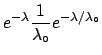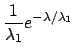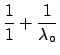Next: Combination of results from
Up: Poisson model: dependence on
Previous: Poisson model: dependence on
Contents
Dependence on priors
The results of Sections ![[*]](file:/usr/lib/latex2html/icons/crossref.png) and
and ![[*]](file:/usr/lib/latex2html/icons/crossref.png) were obtained using a
uniform prior. One may worry how much the result changes
if different priors are used in the analysis.
Bearing in mind the rule of coherence, we are clearly
interested only in
reasonable9.1 priors.
were obtained using a
uniform prior. One may worry how much the result changes
if different priors are used in the analysis.
Bearing in mind the rule of coherence, we are clearly
interested only in
reasonable9.1 priors.
In frontier physics
the choice of
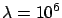 is often not reasonable.
For example, searching for monopoles, one does not
believe that
is often not reasonable.
For example, searching for monopoles, one does not
believe that
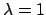 and
and 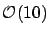 are equally possible.
Realistically, one would expect to observe, with the planned experiment
and running time,
are equally possible.
Realistically, one would expect to observe, with the planned experiment
and running time,
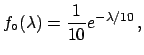 monopoles, if they exist at all.
We follow the same arguments of Section
monopoles, if they exist at all.
We follow the same arguments of Section ![[*]](file:/usr/lib/latex2html/icons/crossref.png) (negative neutrino mass), modelling the prior beliefs
of a community of rational people who have
planned and run the experiment.
For reasons of mathematical convenience, we model
(negative neutrino mass), modelling the prior beliefs
of a community of rational people who have
planned and run the experiment.
For reasons of mathematical convenience, we model
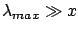 with an exponential, but, extrapolating the results
of Section
with an exponential, but, extrapolating the results
of Section ![[*]](file:/usr/lib/latex2html/icons/crossref.png) , it is easy to understand that
the exact function is not really crucial for the final result.
, it is easy to understand that
the exact function is not really crucial for the final result.
The function
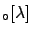 |
(9.1) |
with
may be well suited to the case: the highest beliefs
are for small values of  , but also values
up to 30 or 50 would not be
really surprising.
We obtain the following results:
, but also values
up to 30 or 50 would not be
really surprising.
We obtain the following results:
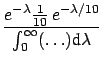 |
 |
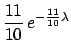 |
(9.2) |
| |
 |
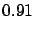 |
(9.3) |
E![$\displaystyle [\lambda]$](img807.png) |
 |
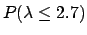 |
|
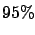 |
 |
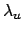 |
|
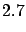 |
 |
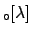 with 95% probability with 95% probability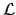 |
(9.4) |
The result is very stable. Changing
E![$ _\circ[\lambda]$](img1300.png) from `
from `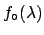 ' to 10 has only a
10% effect on the upper limit. As far as the scientific conclusions
are concerned, the two limit are identical.
For this reason one should not
worry about using a uniform prior, and complicate one's life
to model a more realistic
prior.
' to 10 has only a
10% effect on the upper limit. As far as the scientific conclusions
are concerned, the two limit are identical.
For this reason one should not
worry about using a uniform prior, and complicate one's life
to model a more realistic
prior.
As an exercise, we can extend this result to a generic expected
value of events, still sticking to the exponential:
which has an expected value
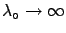 .
The uniform distribution is recovered
for
.
The uniform distribution is recovered
for
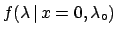 . We get:
. We get:
The upper limit, at a probability level 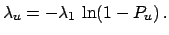 , becomes:
, becomes:
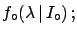 |
(9.5) |




Next: Combination of results from
Up: Poisson model: dependence on
Previous: Poisson model: dependence on
Contents
Giulio D'Agostini
2003-05-15
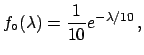 monopoles, if they exist at all.
We follow the same arguments of Section
monopoles, if they exist at all.
We follow the same arguments of Section ![]() is often not reasonable.
For example, searching for monopoles, one does not
believe that
is often not reasonable.
For example, searching for monopoles, one does not
believe that
![]() and
and ![]() are equally possible.
Realistically, one would expect to observe, with the planned experiment
and running time,
are equally possible.
Realistically, one would expect to observe, with the planned experiment
and running time,
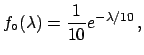 monopoles, if they exist at all.
We follow the same arguments of Section
monopoles, if they exist at all.
We follow the same arguments of Section ![]() (negative neutrino mass), modelling the prior beliefs
of a community of rational people who have
planned and run the experiment.
For reasons of mathematical convenience, we model
(negative neutrino mass), modelling the prior beliefs
of a community of rational people who have
planned and run the experiment.
For reasons of mathematical convenience, we model
![]() with an exponential, but, extrapolating the results
of Section
with an exponential, but, extrapolating the results
of Section ![]() , it is easy to understand that
the exact function is not really crucial for the final result.
, it is easy to understand that
the exact function is not really crucial for the final result.