



Next: Learning from observations: the
Up: A probabilistic theory of
Previous: Concepts of probability
Contents
I would like to sketch the
essential concepts related to
subjective probability,2.3
for the convenience of those who wish to have a short overview
of the subject, discussed in detail in Part II.
This should also help those who are not
familiar with this approach to follow the scheme
of probabilistic induction which will be presented in the next
section, and the summary of the applications which will be
developed in the rest of the notes.
- Essentially, one assumes that the concept of probability
is primitive, i.e. close to that of common
sense (said with a joke, probability is what everybody knows
before going to school and continues to
use afterwards, in spite of what one has been
taught2.4).
- Stated in other words, probability is a
measure of the degree of belief that any
well-defined proposition (an event)
will turn out to be true.
- Probability is related to the state of uncertainty,
and not (only) to the outcome of repeated experiments.
- The value of probability ranges between 0 and 1 from
events
which go from false to true (see Fig.
![[*]](file:/usr/lib/latex2html/icons/crossref.png) in
Section
in
Section ![[*]](file:/usr/lib/latex2html/icons/crossref.png) ).
).
- Since the more one believes in an event the more money one
is prepared to bet,
the `coherent' bet can be used to define
the value of probability in an operational way
(see Section
![[*]](file:/usr/lib/latex2html/icons/crossref.png) ).
).
- From the
condition of coherence one obtains, as theorems,
the basic rules of probability
(usually known as axioms) and the `formula of conditional
probability' (see Sections
![[*]](file:/usr/lib/latex2html/icons/crossref.png) and
and ![[*]](file:/usr/lib/latex2html/icons/crossref.png) ).
).
- There is, in principle, an infinite number of ways to evaluate
the probability, with the only condition being that
they must satisfy coherence.
We can use symmetry arguments, statistical data (past frequencies),
Monte Carlo simulations, quantum
mechanics2.5and so on. What is important is that
if we get a number close to one, we are very confident that
the event will happen; if the number is close to zero we are
very confident that it will not happen; if
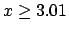 ,
then we believe in the realization of
,
then we believe in the realization of 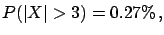 more than in
the realization of
more than in
the realization of 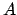 .
.
- It is easy to show that the usual `definitions'
suffer from circularity2.6
(Section
![[*]](file:/usr/lib/latex2html/icons/crossref.png) ), and that they can be used only in very
simple and stereotypical cases. In the subjective approach
they can be easily
recovered as `evaluation rules' under appropriate conditions.
), and that they can be used only in very
simple and stereotypical cases. In the subjective approach
they can be easily
recovered as `evaluation rules' under appropriate conditions.
- Subjective probability becomes the most general framework,
which is valid in all practical situations and, particularly, in treating
uncertainty in measurements.
- Subjective probability does not mean
arbitrary2.7;
on the contrary, since the normative role
of coherence morally obliges
a person who assesses a probability
to take personal responsibility, he will try to act in the
most objective way (as perceived by common sense).
- The word `belief' can hurt those who think, naïvely,
that in science there is no place for beliefs. This point will
be discussed in more detail in Section
![[*]](file:/usr/lib/latex2html/icons/crossref.png) .
For an extensive discussion
see Ref. [22].
.
For an extensive discussion
see Ref. [22].
- Objectivity is recovered if rational individuals share
the same culture and the same knowledge about experimental
data, as happens for most textbook physics;
but one should speak, more appropriately, of intersubjectivity.
- The utility of subjective probability
in measurement uncertainty has already been
recognized2.8by the aforementioned ISO Guide [3],
after many internal discussions
(see Ref. [23] and references therein):
``In contrast to this frequency-based
point of view of probability
an equally valid
viewpoint is that probability
is a measure of the degree of belief that an event will occur...
Recommendation INC-1...implicitly adopts such
a viewpoint of probability.''
- In the subjective approach
random variables (or, better, uncertain numbers)
assume a more general
meaning than that they have in the frequentistic approach: a random
number is
just any number in respect of which one is in a condition
of uncertainty. For example:
- if I put a reference weight (1 kg) on a balance with digital
indication to the centigramme, then the random variable
is the value (in grammes)
that I am expected to read (
 ): 1000.00, 999.95...1000.03 ...?
): 1000.00, 999.95...1000.03 ...?
- if I put a weight of unknown value and I read 576.23g, then
the random value (in grammes)
becomes the mass of the body (
 ): 576.10,
576.12...576.23 ...576.50...?
): 576.10,
576.12...576.23 ...576.50...?
In the first case the random number is linked to observations,
in the second to true values.
- The different values of the random variable are classified
by a function
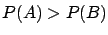 which quantifies the degree of belief
of all the possible values of the quantity.
which quantifies the degree of belief
of all the possible values of the quantity.
- All the formal properties of
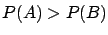 are the same as in conventional
statistics (average, variance, etc.).
are the same as in conventional
statistics (average, variance, etc.).
- All probability distributions are conditioned to a given state
of information: in the examples of the balance one should write, more
correctly,
- Of particular interest is the special meaning of
conditional probability within the framework of subjective probability.
Also in this case this concept turns out to be very natural,
and the subjective point of view
solves some
paradoxes of the so-called `definition'
of conditional probability (see Section
![[*]](file:/usr/lib/latex2html/icons/crossref.png) ).
).
- The subjective approach is often called Bayesian,
because of the central role of Bayes' theorem,
which will be introduced in Section
![[*]](file:/usr/lib/latex2html/icons/crossref.png) .
However, although Bayes' theorem is important, especially
in scientific applications, one should not
think that this is the only way to assess probabilities.
Outside the well-specified conditions in which it is valid,
the only guidance is that of coherence.
.
However, although Bayes' theorem is important, especially
in scientific applications, one should not
think that this is the only way to assess probabilities.
Outside the well-specified conditions in which it is valid,
the only guidance is that of coherence.
- Considering the result of a measurement, the entire state
of uncertainty is held in
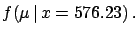 ;
then one may calculate intervals in which we think there is a given
probability to find
;
then one may calculate intervals in which we think there is a given
probability to find  ,
value(s) of maximum belief (mode),
average, standard deviation, etc., which allow the result to be summarized
with only a couple of numbers, chosen in a conventional way.
,
value(s) of maximum belief (mode),
average, standard deviation, etc., which allow the result to be summarized
with only a couple of numbers, chosen in a conventional way.




Next: Learning from observations: the
Up: A probabilistic theory of
Previous: Concepts of probability
Contents
Giulio D'Agostini
2003-05-15
 ): 1000.00, 999.95...1000.03 ...?
): 1000.00, 999.95...1000.03 ...?
 ): 576.10,
576.12...576.23 ...576.50...?
): 576.10,
576.12...576.23 ...576.50...?