



Next: Evaluation of type B
Up: Approximate methods
Previous: Linearization
Contents
In this section we compare the results obtained in the previous
section with the recommendations of the Bureau International des Poids
et Mesures (BIPM) and the International Organization for Standardization
(ISO) on ``the expression of experimental uncertainty''.
The uncertainty in the result of a measurement generally consists
of several components which may be grouped into two categories according
to the way in which their numerical value is estimated:
- A:
- those which are evaluated by statistical methods;
- B:
- those which are evaluated by other means.
There is not always a simple correspondence between the classification into
categories A or B and the previously used classification into
``random'' and ``systematic'' uncertainties.
The term ``systematic uncertainty'' can be misleading
and should be avoided.
The detailed report of the uncertainty should
consist of a complete list of the components, specifying for each the
method used to obtain its numerical result.
Essentially
the first recommendation states that all uncertainties
can be treated probabilistically. The distinction between types A and B
is subtle and can be misleading if one thinks of ``statistical
methods'' as synonymous with ``probabilistic methods'', as is currently
the case in High Energy Physics.
Here ``statistical'' has the classical meaning of
repeated measurements.
The components in category A are characterized by the estimated
variances 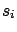 (or the estimated ``standard deviations''
(or the estimated ``standard deviations'' 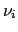 )
and the number of degrees of freedom
)
and the number of degrees of freedom 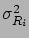 . Where appropriate,
the covariances should be given.
. Where appropriate,
the covariances should be given.
The estimated variances correspond to
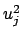 of the
previous section. The degrees of freedom are related to small
samples and to the Student t distribution. The problem of
small samples is not discussed in these notes,
but clearly this recommendation
is a relic of frequentistic methods. With the approach followed in
these notes
there is no need to talk about degrees of freedom,
since the Bayesian inference defines the final
probability function
of the
previous section. The degrees of freedom are related to small
samples and to the Student t distribution. The problem of
small samples is not discussed in these notes,
but clearly this recommendation
is a relic of frequentistic methods. With the approach followed in
these notes
there is no need to talk about degrees of freedom,
since the Bayesian inference defines the final
probability function 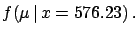 completely6.2.
completely6.2.
The components in category B should be characterized
by quantities 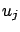 , which may be considered as approximations
to the corresponding variances, the existence of which is assumed. The
quantities
, which may be considered as approximations
to the corresponding variances, the existence of which is assumed. The
quantities 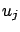 may be treated like variances and the quantities
may be treated like variances and the quantities
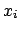 like standard deviations. Where appropriate,
the covariances should be treated in a similar way.
like standard deviations. Where appropriate,
the covariances should be treated in a similar way.
Clearly, this
recommendation is meaningful only in a Bayesian framework.
The combined uncertainty should be characterized by the numerical
value obtained by applying the usual method for the combination
of variances. The combined uncertainty and its components should
be expressed in the form of ``standard deviations''.
This is
what we have found in (![[*]](file:/usr/lib/latex2html/icons/crossref.png) ) and (
) and (![[*]](file:/usr/lib/latex2html/icons/crossref.png) ).
).
If, for particular applications, it is necessary to multiply
the combined uncertainty by a factor to obtain
an overall uncertainty, the multiplying factor used must always be
stated.
This last recommendation states once more that the uncertainty is ``by
default'' the standard deviation
of the true value distribution. Any other quantity
calculated
to obtain a credibility interval with a certain
probability level should be clearly stated.
To summarize, these are the basic ingredients of
the BIPM/ISO recommendations.
- subjective definition of probability:
- it allows variances to
be assigned conceptually to any physical quantity
which has an uncertain value;
- uncertainty as standard deviation
-
- it is ``standard'';
- the rule of combination
(
![[*]](file:/usr/lib/latex2html/icons/crossref.png) )-(
)-(![[*]](file:/usr/lib/latex2html/icons/crossref.png) ) applies to standard deviations and not
to confidence intervals;
) applies to standard deviations and not
to confidence intervals;
- combined standard uncertainty:
- it is obtained by the usual formula
of ``error propagation'' and it makes use of variances,
covariances and first derivatives;
- central limit theorem:
- it makes, under proper conditions,
the true value
normally distributed if one has several sources of uncertainty.
Consultation of the Guide[3]
is recommended
for further explanations about the justification of the standards,
for the
description of evaluation procedures, and for examples.
I would just like to
end this section with some examples of the evaluation of
type B uncertainties and with some words of caution
concerning the use of approximations and of linearization.




Next: Evaluation of type B
Up: Approximate methods
Previous: Linearization
Contents
Giulio D'Agostini
2003-05-15
(or the estimated ``standard deviations''
) and the number of degrees of freedom
. Where appropriate, the covariances should be given.
, which may be considered as approximations to the corresponding variances, the existence of which is assumed. The quantities
may be treated like variances and the quantities
like standard deviations. Where appropriate, the covariances should be treated in a similar way.