Building the covariance matrix of experimental data

In physics applications, it is rarely the case that the covariance between the best estimates of two physical quantities^6.7, each given by the arithmetic average of direct measurements ( $x_i = \overline{X_i} = \frac{1}{n}\sum_{k=1}^n X_{ik}$), can be evaluated from the sample covariance^6.8 of the two averages:

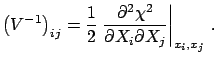$$(x_i,x_j) =\frac{1}{n\,(n-1)}\sum_{k=1}^{n}(X_{ik}-\overline{X}_i)(X_{jk}-\overline{X}_j)\ .$$ (6.23)

More frequent is the well-understood case in which the physical quantities are obtained as a result of a $\chi^2$ minimization, and the terms of the inverse of the covariance matrix are related to the curvature of $\chi^2$ at its minimum:

$$\left(V^{-1}\right)_{ij} = \frac{1}{2}\left. \frac{\partial^2\chi^2}{\partial X_i\partial X_j} \right\vert _{x_i,x_j}\, .$$ (6.24)

In most cases one determines independent values of physical quantities with the same detector, and the correlation between them originates from the detector calibration uncertainties. Frequentistically, the use of () in this case would correspond to having a ``sample of detectors'', each of which is used to perform a measurement of all the physical quantities.

A way of building the covariance matrix from the direct measurements is to consider the original measurements and the calibration constants as a common set of independent and uncorrelated measurements, and then to calculate corrected values that take into account the calibration constants. The variance/covariance propagation will automatically provide the full covariance matrix of the set of results. Let us derive it for two cases that occur frequently, and then proceed to the general case.