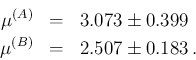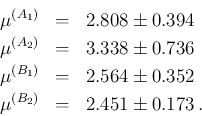Imagine we have a sample of 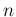 observations, characterized
by independent Gaussian errors with unkown
observations, characterized
by independent Gaussian errors with unkown 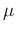 ,
associated to the true value of interest, and also unkown
,
associated to the true value of interest, and also unkown 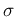 .
Our main interest is to infer
.
Our main interest is to infer 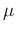 , but in this case also
, but in this case also 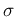 needs to be estimated from the same sample. The `estimators' (to use
frequentistic vocabulary, to which most readers are most likely
familiar)
of
needs to be estimated from the same sample. The `estimators' (to use
frequentistic vocabulary, to which most readers are most likely
familiar)
of 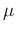 and
and 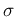 are the aritmetic mean
are the aritmetic mean 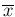 and
the standard deviation
and
the standard deviation 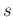 calculated from the sample,
respectively.19In particular the `error' on
calculated from the sample,
respectively.19In particular the `error' on 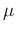 is calculated as
is calculated as
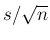 (hereafter we focus on the determination
of
(hereafter we focus on the determination
of 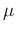 , although a similar reasoning and a related puzzle
concerns the determination of
, although a similar reasoning and a related puzzle
concerns the determination of 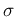 ).
).
Now the question is what happens if we devide the samples in sub-samples,
`determine' 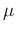 from each sub-sample and then
combine the partial results. In order to avoid abstract
speculations, let us concentrate on the following simulated
sample:20
from each sub-sample and then
combine the partial results. In order to avoid abstract
speculations, let us concentrate on the following simulated
sample:20
|
2.691952 |
2.805799 |
3.826049 |
1.908438,
3.844093 |
2.406228 |
5.176920 |
1.925284 |
|
|
1.688440 |
2.309165 |
3.046256 |
3.211285,
2.302760 |
2.966700 |
2.301784 |
2.232128
|
|
From the aritmetic average (2.7902) and the `empirical'
standard deviation (0.8970), we get
(the exaggerate number of decimal digits, with respect
to reasonable standards, is only to make comparisons easier).
Let us now split the values into two sub-samples (first and second
row, respectively). The `determinations' of 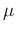 are now
are now
Combining then the two results calculating the weighted average
and its standard deviation, we get
sensibly different from 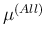 calculated above.
calculated above.
We can then split again the two samples (first four values and
second four values of each row), thus getting
Combining the four partial results we get then
different from 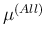 and from
and from 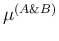 .
.
What is going on? Or, more precisely,
what should be the combination rule such that
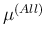 ,
, 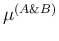 and
and
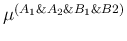 would be the same?
(Sufficient hints are in the paper
and a note could possibly follow with a detailed treatement of the case.)
would be the same?
(Sufficient hints are in the paper
and a note could possibly follow with a detailed treatement of the case.)
![]() from each sub-sample and then
combine the partial results. In order to avoid abstract
speculations, let us concentrate on the following simulated
sample:20
from each sub-sample and then
combine the partial results. In order to avoid abstract
speculations, let us concentrate on the following simulated
sample:20
![]() are now
are now