As it is well known, the standard deviation of a weighted average
depends only on the individual standard deviations, but not
on the dispersion of the values around the
mean.
This property leads sometimes to the
embarrassing situation in which the combined result
`looks' somehow at odds with the individual ones.
A practical way to cure the problem is to enlarge
the resulting standard deviation by the
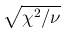
scaling, a
prescription employed with arbitrary criteria on when to apply it and
which individual results to use in the combination.
But the `apparent' discrepancy between the combined result
and the individual ones often remains. Moreover this rule does not
affect the resulting `best value', even if the pattern of the
individual results is highly skewed.
In addition to these reasons of dissatisfaction, shared by many practitioners,
the method causes another issue,
recently noted on the published measurements
of the charged kaon mass.
It happens in fact that, if the prescription is applied twice,
i.e. first to a sub-sample of the individual results and subsequently
to the entire sample, then
a bias on the result of the overall combination
is introduced. The reason is that the prescription does not
guaranty
statistical sufficiency, whose importance is reminded
in this script, written with a didactic spirit, with some historical notes
and with a language to which most physicists are accustomed.
The conclusion contains general remarks on the effective
presentation of the experimental findings and a pertinent
puzzle
is proposed in the Appendix.