Possibly discrepant results
Well known features of the combination
of measurements by the weighted
average, reminded in the last section, are that i) the combined result
has a “degree of precision” [1]
higher than each of the individual contributions
or, in terms of standard deviations,
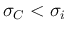 ;
ii) the resulting standard deviation
does not depend on the spread of the individual
results around the mean value;
iii) the error model of the `equivalent observation'
remains Gaussian. However, it is a matter of fact that,
although from the probabilistic point of view
there is no contradiction with the basic assumptions, since
patterns of individual results `oddly' scattered around their average
have some chance to occur, we sometimes suspect that
there it might be something `odd' going on. That is, we
tend to doubt on the validity of the simple model of Gaussian errors with
the declared “degrees of precision”.
(But someone might start to worry
too early,10 sometimes even driven by
wishful thinking, that is she hopes,
rather than believes, that the reason of disagreement might be
caused by new phenomenology or violation
of fundamental laws of physics
[8,9].)
;
ii) the resulting standard deviation
does not depend on the spread of the individual
results around the mean value;
iii) the error model of the `equivalent observation'
remains Gaussian. However, it is a matter of fact that,
although from the probabilistic point of view
there is no contradiction with the basic assumptions, since
patterns of individual results `oddly' scattered around their average
have some chance to occur, we sometimes suspect that
there it might be something `odd' going on. That is, we
tend to doubt on the validity of the simple model of Gaussian errors with
the declared “degrees of precision”.
(But someone might start to worry
too early,10 sometimes even driven by
wishful thinking, that is she hopes,
rather than believes, that the reason of disagreement might be
caused by new phenomenology or violation
of fundamental laws of physics
[8,9].)
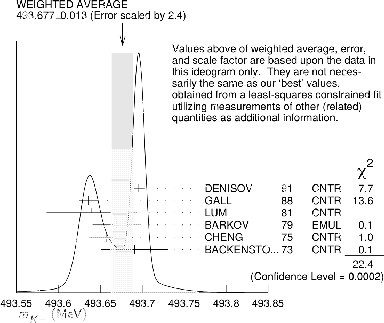
Figure:
Charged kaon mass from several experiments
as summarized by the PDG [7]. Note that besides
the `error' of 0.013 MeV,
obtained by a 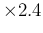 scaling,
also an `error' of 0.016 MeV is provided,
obtained by a
scaling,
also an `error' of 0.016 MeV is provided,
obtained by a 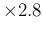 scaling. The two results are
called `OUR AVERAGE' and 'OUR FIT', respectively [7].
scaling. The two results are
called `OUR AVERAGE' and 'OUR FIT', respectively [7].
 |
In the case we have serious suspicions about the
presence of other effects, then
we should change our model, make a new analysis and accept its outcome
in the light of clearly stated hypotheses and
conditions [2,3,4].
As a result, not only the overall `error'11 should change, but also the
shape of the final distribution should, since there is no strong
reason to remain Gaussian.
For example, the final distribution
might be skewed or even multimodal [2],
as it should be desirable
if the pattern of individual measurements
suggest so. In particular,
the most probable value (mode) will differ from the
average of the distribution and from the median.
Instead, traditionally, only the
`error' is enlarged by an arbitrary factor
depending on the frequentistic `test variable' 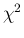 ,
namely
,
namely
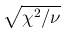 , where
, where 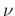 stands for the number of
degrees of freedom.
But the central value is
kept unchanged and the interpretation of the result, explicitly stated
or implicitly assumed so
in subsequent analyses by other scientists,
remains Gaussian.12
stands for the number of
degrees of freedom.
But the central value is
kept unchanged and the interpretation of the result, explicitly stated
or implicitly assumed so
in subsequent analyses by other scientists,
remains Gaussian.12
As a practical example, let us take the results concerning the
charged kaon mass of Fig. 2 and Tab. 1, as selected by the PDG [7].
Figure:
Graphical representation of the results on the charged kaon mass
of Tab. 1 (solid blue Gaussians).
The dashed red Gaussian shows the result
of the standard combination obtained by the weighted average.
The solid gray Gaussian, centered with the dashed red one,
shows the broadening due to
the
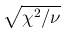 prescription (see text).
prescription (see text).
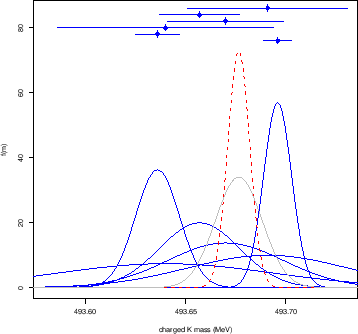 |
From the weighted average and its
standard deviation
we get
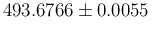 MeV,
shown in Fig. 3 by the dashed red Gaussian
(the solid blue Gaussians depict the results of the six
results of Tab. 1. Comparing the individual results with the weighted average
we calculate
a
MeV,
shown in Fig. 3 by the dashed red Gaussian
(the solid blue Gaussians depict the results of the six
results of Tab. 1. Comparing the individual results with the weighted average
we calculate
a 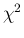 of 22.9, and hence a scaling factors of 2.14, getting
then
of 22.9, and hence a scaling factors of 2.14, getting
then
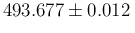 MeV, reported
on the same figure by the solid gray Gaussian below the
dashed one.13The two results are reported also in the entry A of
the summary table 3.
MeV, reported
on the same figure by the solid gray Gaussian below the
dashed one.13The two results are reported also in the entry A of
the summary table 3.

