- ...
cancel,1
-
“It is of the greatest importance, that the several positions
of the heavenly body on which it is proposed to base the orbit,
should not be
taken from single observations, but, if possible,
from several so combined that the accidental errors might,
as far as may be, mutually destroy
each other.” [1]
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... information.2
- For example Gauss discusses the implications
of averaging observations over days or weeks, during which
the heavenly body has certainly changed position in the elapsed time.
But the mean position in the mean time can be considered as an
equivalent point in space and time, and a few of them, far apart,
would be enough to determine the orbit parameters.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... features.3
- The network
of all quantities
involved in the model is also known
as Bayesian network for two reasons: degrees of belief
are assigned to all variables in the game (even to the observed
ones, meant as conditional probabilities depending on the
value of the others); inference and
forecasting (the names are related
to the purposes of our analysis - from the probabilistic point of
view there is no difference) are then
made by the use of probability rules, in particular
the so called Bayes' rule, without the
need to invent prescriptions or ad hoc `principles'.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... issues.4
- This
is not the case, at the moment,
for the charged kaon mass, as commented in Ref. [2],
especially footnote 19.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... factors,5
- This is related to the
so called Likelihood Principle, which is consider
a good feature by frequentists,
though not all frequentistic methods
respect it [5].
In practice, it says that the result of an inference should not
depend on multiplicative factors of the likelihood functions.
This `principle' arises automatically in a probabilistic
(`Bayesian') framework.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... `flat',6
- I refer again to footnote 9
of Ref. [2], reminding that
the Princeps Mathematicorum
derived the `Gaussian' as the error function such that the
maximum of the posterior for a flat `prior' (explicitly stated)
had a maximum corresponding to the arithmetic average of the observations,
provided they were independent and they had
“the same level of accuracy”.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... value7
- Citing again
Gauss, he wrote explicitly of most
probable value of `
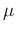 ', under the hypothesis that
before the experiment all its values were equally
probable [1].
', under the hypothesis that
before the experiment all its values were equally
probable [1].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... likelihood;8
- Hence the famous Maximum likelihood
`principle', which is then nothing but a simple case of the more general
probabilistic approach. (But the value
that maximizes the likelihood is not necessarily the best
value to report, as it will be commented in the conclusions.)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...; 9
- And it is easy to recognize,
in this sub-case of the general
probabilistic
approach, another famous `principle'.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... early,10
- It is rather
well known that the human mind has problems when
dealing with randomness. For example, if you ask a person
to write, at random, a long list of 0's and 1's,
she will tend to `regularize' the series, which will then
contain only short sequences of 0's and 1's,
contrary to what happens rolling a coin, or using a
(pseudo-)random generator. As an interesting book that
discusses, among others, this experimental fact,
Ref. [12] is recommended.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... `error'11
- The
quote marks are to remind
that they refer, more precisely,
to standard uncertainty,
referring the nouns error and uncertainty
to different concepts [10,11].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Gaussian.12
- For example, the bimodal
curve shown in the ideogram of Fig. 2
is a curious linear combination of Gaussians
of
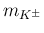 , although from a frequentistic point
of view one should not be allowed to attribute probabilities, and hence
pdf's, to true values. And there are even frequentistic `gurus'
who use probability in quote marks, without explaining the reason but
because they are aware that could not talk about probability, when they write
“When the result of a measurement of a physical quantity
is published as
, although from a frequentistic point
of view one should not be allowed to attribute probabilities, and hence
pdf's, to true values. And there are even frequentistic `gurus'
who use probability in quote marks, without explaining the reason but
because they are aware that could not talk about probability, when they write
“When the result of a measurement of a physical quantity
is published as
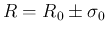 without further explanation, it is implied
that R is a gaussian-distributed measurement with mean
without further explanation, it is implied
that R is a gaussian-distributed measurement with mean 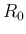 and variance
and variance 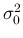 . This allows one to calculate
various confidence intervals of given “probability”, i.e.,
the “probability”
. This allows one to calculate
various confidence intervals of given “probability”, i.e.,
the “probability” 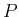 that the true value of
that the true value of 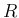 is withing a given interval.” [13].
is withing a given interval.” [13].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... one.13
- Besides rounding, the numbers slightly differ from those
of Ref. [7], having applied there some
ad hoc selections. But this does not
change the essence of the message this note desires to convey.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
average.14
- Then the PDG adds a more intriguing curve
n the reported `ideograms'[7] (see e.g.
Fig. 1 of Ref. [2]). But this non-Gaussian
curve
has no probabilistic meaning,
as discussed in [2], and, anyway,
it is not used to draw no quantitative
results, as far as I understand (and I hope...).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... one.15
- It seems that people
are worried only if the `errors' appear small.
But, as also stated by the ISO Guide [10],
“Uncertainties in measurements” should
be “realistic rather than safe”.
In particular the method recommended by the ISO Guide
“stands [...] in contrast to certain older methods that have
the following two ideas in common:
- The first idea is that the uncertainty reported should be
`safe' or `conservative [...] In fact, because the evaluation of the
uncertainty of a measurement result is problematic, it was often
made deliberately large. [...]”
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... scaling16
- The shift of the
average almost in the middle of the two most precise results makes
the contributions to the
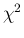 huge. Here are the differences
of the individual measurements in unit of their standard deviations:
huge. Here are the differences
of the individual measurements in unit of their standard deviations:
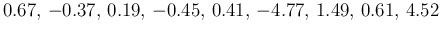 ,
resulting in a
,
resulting in a 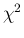 of 46.7 and a consequent p-value of
of 46.7 and a consequent p-value of
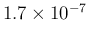 .
Therefore, also to whom who are critical against
p-values [8,9],
in a case of this kind, an alarm bell should sound [21].
But to all persons of good sense a similar alarm,
concerning the frequentist solution of the problem,
should sound too (see Ref. [2]
for a sceptical alternative.)
.
Therefore, also to whom who are critical against
p-values [8,9],
in a case of this kind, an alarm bell should sound [21].
But to all persons of good sense a similar alarm,
concerning the frequentist solution of the problem,
should sound too (see Ref. [2]
for a sceptical alternative.)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
beliefs17
- As the historian of science Peter Galison puts it,
“Experiments begin and end in a matrix of beliefs.
...beliefs in instrument type, in programs of experiment
inquiry, in the trained, individual judgments about every local behavior
of pieces of apparatus.” [22].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... function.18
- In the case
there are only some possibilities, or we are interested
on how the data support an hypothesis over others,
the quantity to report is (are) the likelihood ratio(s),
as recently recognized also by the European Network of Forensic Science
Institutes (ENFSI) [25]. Note that a likelihood function,
or likelihood ratios (also known as Bayes factors), cannot
be considered as `objective numbers', because they depend
on the judgments of experts. This is also recognized by the
ENFSI Guidelines [25], which appears then rather
advanced with respect to naive ideals of objectivism that often
are instead just a defense of established procedures and methods
supported by inertia and authority.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
respectively.19
- See e.g. Sec. 39.2.1 of Ref
[7],
http://pdg.lbl.gov/2019/reviews/rpp2019-rev-statistics.pdf
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
sample:20
- The sample has been obtained
with the Gaussian random number generator rnorm()
of the R language[30], with the following commands
set.seed(20200102)
n = 16; mu = 3; sigma = 1
x = rnorm(n, mu, sigma)
so that we know the `true 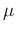 '.
(The random seed, used to make the
numbers reproducible, was set to the date in which
the sample was generated.) Mean and standard deviation
are then calculated using R functions:
'.
(The random seed, used to make the
numbers reproducible, was set to the date in which
the sample was generated.) Mean and standard deviation
are then calculated using R functions:
m = mean(x)
s = sd(x)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.