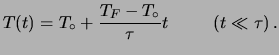Next: Ipotesi effettuate nella precedente
Up: Esercitazione di termologia
Previous: Scopo dell'esercitazione
Indice
Il calore scambiato nell'unità di tempo da un termometro
con il fluido in cui è immerso è proporzionale alla differenza
istantanea
di temperatura fra termometro e fluido:
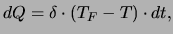 |
(3) |
dove 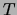 rappresenta la temperatura istantanea del termometro
e
rappresenta la temperatura istantanea del termometro
e 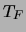 quella del fluido (quest'ultima è supposta costante
durante le misure).
Il fattore di
proporzionalità
quella del fluido (quest'ultima è supposta costante
durante le misure).
Il fattore di
proporzionalità 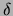 dipende dalla superficie di contatto,
dallo spessore della parete di vetro e
dalla conducibilità termica del
vetro, del mercurio e del fluido. In consequenza
dello scambio di calore il termometro
subisce una variazione di temperatura proporzionale al calore scambiato
e inversamente proporzionale alla sua capacità termica:
dipende dalla superficie di contatto,
dallo spessore della parete di vetro e
dalla conducibilità termica del
vetro, del mercurio e del fluido. In consequenza
dello scambio di calore il termometro
subisce una variazione di temperatura proporzionale al calore scambiato
e inversamente proporzionale alla sua capacità termica:
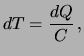 |
(4) |
dove 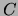 rappresenta la capacità termica del termometro.
Combinando la (1) con la (2) si trova l'equazione differenziale
che descrive l'evoluzione nel tempo della temperatura del termometro:
rappresenta la capacità termica del termometro.
Combinando la (1) con la (2) si trova l'equazione differenziale
che descrive l'evoluzione nel tempo della temperatura del termometro:
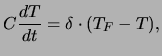 |
(5) |
la cui soluzione è:
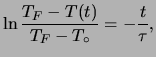 |
(6) |
dove si è chiamato 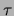 il rapporto
il rapporto
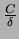 .
Dalla (4) segue:
.
Dalla (4) segue:
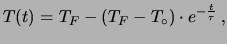 |
(7) |
con
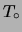 la temperatura del termometro
all'istante
la temperatura del termometro
all'istante  di inizio delle misure
(che non è necessariamente l'istante
di immersione del termometro nel fluido).
Il parametro
di inizio delle misure
(che non è necessariamente l'istante
di immersione del termometro nel fluido).
Il parametro 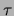 che interviene in andamenti
esponenziali è genericamente chiamato
costante di tempo2
del termometro e ha il
significato fisico di tempo impiegato affiché
la differenza fra il valore della grandezza fisica
e il suo valore asintotico si riduca di
che interviene in andamenti
esponenziali è genericamente chiamato
costante di tempo2
del termometro e ha il
significato fisico di tempo impiegato affiché
la differenza fra il valore della grandezza fisica
e il suo valore asintotico si riduca di 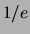 .
Nel nostro caso esso rappresenta quindi il tempo
che occorre al
termometro
per ridurre di
.
Nel nostro caso esso rappresenta quindi il tempo
che occorre al
termometro
per ridurre di 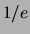 (
(
 ) la differenza di
temperatura iniziale rispetto al fluido (supposto di capacità termica
infinita). Ponendo
) la differenza di
temperatura iniziale rispetto al fluido (supposto di capacità termica
infinita). Ponendo  nella (5) si ottiene infatti:
nella (5) si ottiene infatti:
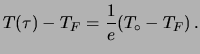 |
(8) |
Poiché la costante di
tempo dei termometri in dotazione è piuttosto piccola,
risulta difficile misurare l'andamento temporale 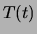 con un cronometro manuale. Per verificare
la legge (5) è quindi opportuno aumentare artificialmente
la costante di tempo
coprendo il
bulbo del termometro con un cappuccetto di gomma
il quale aumenta
con un cronometro manuale. Per verificare
la legge (5) è quindi opportuno aumentare artificialmente
la costante di tempo
coprendo il
bulbo del termometro con un cappuccetto di gomma
il quale aumenta 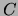 e
diminuisce
e
diminuisce 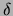 . Questo vuol dire che la costante
di tempo risultante non è quella che si sarebbe
voluta misurare,
ma quella del termometro modificato. Questo artificio è
comunque importante in quanto ci permette di verificare
l'andamento esponenziale e quindi, assumendolo valido,
ci consente di determinare
. Questo vuol dire che la costante
di tempo risultante non è quella che si sarebbe
voluta misurare,
ma quella del termometro modificato. Questo artificio è
comunque importante in quanto ci permette di verificare
l'andamento esponenziale e quindi, assumendolo valido,
ci consente di determinare 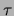 anche qualora
non sia agevole osservare tale l'andamento.
anche qualora
non sia agevole osservare tale l'andamento.
Quindi, per la determinazione di 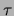 possiamo
considerare tre diversi casi:
possiamo
considerare tre diversi casi:
- A:
- misura dell'andamento
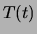 (valori di
(valori di 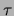 da 20-30 secondi
a qualche minuto): dal grafico su carta semilog di
da 20-30 secondi
a qualche minuto): dal grafico su carta semilog di
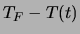 (o di
(o di 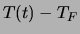 qualora
qualora
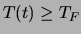 )
in funzione di
)
in funzione di 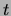 si ricava la costante
di tempo
dal coefficiente angolare, legato a
si ricava la costante
di tempo
dal coefficiente angolare, legato a 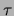 da
da 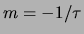 .
.
- B:
- valori di
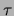 inferiori a una decina di secondi:
non essendo possibile misurare l'andamento di
inferiori a una decina di secondi:
non essendo possibile misurare l'andamento di 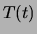 con
i mezzi a disposizione si determina
con
i mezzi a disposizione si determina 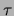 dal tempo impiegato
dal termometro a subire una certa variazione di temperatura
e facendo uso della legge (4).
dal tempo impiegato
dal termometro a subire una certa variazione di temperatura
e facendo uso della legge (4).
- C:
- valori di
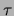 ``molto grandi'' (oltre le decine di minuti),
ovvero le misure vengono effettuate in un intervallo di tempo
molto minore di
``molto grandi'' (oltre le decine di minuti),
ovvero le misure vengono effettuate in un intervallo di tempo
molto minore di 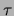 . Ne segue che
l'andamento di
. Ne segue che
l'andamento di
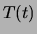 è circa lineare nell'intervallo temporale
di interesse, come si può vedere
facilmente espandendo
è circa lineare nell'intervallo temporale
di interesse, come si può vedere
facilmente espandendo
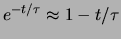 ,
se
,
se  . Ne segue:
. Ne segue:
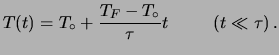 |
(9) |
( Sarà questo il caso della costante di tempo
che caratterizza
la termalizzazione
del calorimetro verso l'ambiente esterno.)
In questo caso la costante di tempo
può essere ricavata graficamente riportando l'andamento 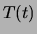 su carta lineare. Si noti che anche in questa misura
è importante la conoscenza di
su carta lineare. Si noti che anche in questa misura
è importante la conoscenza di 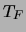 : la derivata
: la derivata 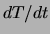 non
è sufficiente per ottenere la costante di tempo.
non
è sufficiente per ottenere la costante di tempo.
E' ovvio che il metodo B può essere utilizzato
anche nei casi in cui il risultato può
essere ottenuto con metodi grafici nei casi A e C.
Si noti comunque che una delle differenza fra il metodo B
e gli altri due è che in questo si utilizzano soltanto
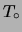 e
e 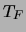 e un valore intermedio, mentre negli altri
metodi si utilizzano molti valori
intermedi. I risultati dei
metodi A e C saranno - per così dire - più ``stabili''
dell'altro metodo. Quindi, quando si usa il metodo
e un valore intermedio, mentre negli altri
metodi si utilizzano molti valori
intermedi. I risultati dei
metodi A e C saranno - per così dire - più ``stabili''
dell'altro metodo. Quindi, quando si usa il metodo 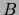 è
opportuno ripetere più volte le misure al fine di ottenere
un valore medio che - intuitivamente -
dovrebbe essere più stabile
di quello ottenuto
nella singola misura.
è
opportuno ripetere più volte le misure al fine di ottenere
un valore medio che - intuitivamente -
dovrebbe essere più stabile
di quello ottenuto
nella singola misura.
Subsections




Next: Ipotesi effettuate nella precedente
Up: Esercitazione di termologia
Previous: Scopo dell'esercitazione
Indice
Giulio D'Agostini
2001-04-02
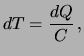
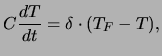
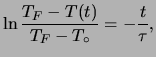
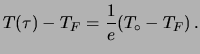
![]() con un cronometro manuale. Per verificare
la legge (5) è quindi opportuno aumentare artificialmente
la costante di tempo
coprendo il
bulbo del termometro con un cappuccetto di gomma
il quale aumenta
con un cronometro manuale. Per verificare
la legge (5) è quindi opportuno aumentare artificialmente
la costante di tempo
coprendo il
bulbo del termometro con un cappuccetto di gomma
il quale aumenta ![]() e
diminuisce
e
diminuisce ![]() . Questo vuol dire che la costante
di tempo risultante non è quella che si sarebbe
voluta misurare,
ma quella del termometro modificato. Questo artificio è
comunque importante in quanto ci permette di verificare
l'andamento esponenziale e quindi, assumendolo valido,
ci consente di determinare
. Questo vuol dire che la costante
di tempo risultante non è quella che si sarebbe
voluta misurare,
ma quella del termometro modificato. Questo artificio è
comunque importante in quanto ci permette di verificare
l'andamento esponenziale e quindi, assumendolo valido,
ci consente di determinare ![]() anche qualora
non sia agevole osservare tale l'andamento.
anche qualora
non sia agevole osservare tale l'andamento.
![]() possiamo
considerare tre diversi casi:
possiamo
considerare tre diversi casi: