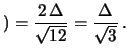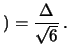Next: Valutazione dell'incertezza di misura:
Up: Errori e incertezze di
Previous: Probabilità soggettiva
Indice
Prima di procedere alle applicazioni, ricordiamo brevemente
la terminologia
sulle variabili casuali (nel linguaggio della probabilità
soggettiva).
- Una variabile casuale, o numero aleatorio,
è qualsiasi numero rispetto al quale si è in stato di incertezza.
Facciamo due esempi nel contesto delle misure:
- Pongo un chilogrammo campione su una bilancia di laboratorio con indicazione
(digitale) dei centesimi. Che valore leggerò (in grammi)? 1000.00, 999.95,
1000.03 ...?
- Leggo su una bilancia di laboratorio 2.315 g. Quanto vale il valore vero
della massa del corpo? 2.311, 2.312, ...2.315, ...2.319, ...?
Nel primo caso la variabile è la lettura 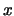 (subordinatamente
ad un certo valore vero); nel secondo caso la variabile è il valore
vero
(subordinatamente
ad un certo valore vero); nel secondo caso la variabile è il valore
vero 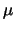 (subordina-tamente
ad un certo valore letto).
(subordina-tamente
ad un certo valore letto).
- Ai possibili valori della grandezza viene associata una funzione
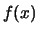 che quantifica il grado di fiducia ad essi assegnato.
Quindi scrivere che
che quantifica il grado di fiducia ad essi assegnato.
Quindi scrivere che
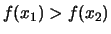 sta ad
indicare che si crede più a
sta ad
indicare che si crede più a 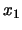 che a
che a 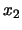 .
A seconda che la variabile
.
A seconda che la variabile 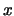 sia discreta
o continua,
sia discreta
o continua, 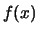 ha l'accezione
di funzione di probabilità o di
funzione densità di probabilità.
ha l'accezione
di funzione di probabilità o di
funzione densità di probabilità.
- Tutte le proprietà di
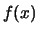 apprese nei corsi convenzionali
rimangono valide nell'approccio
soggettivista. In particolare si ricorda che il valore atteso,
indicato con
E
apprese nei corsi convenzionali
rimangono valide nell'approccio
soggettivista. In particolare si ricorda che il valore atteso,
indicato con
E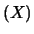 e
calcolato come media dei possibili valori di
e
calcolato come media dei possibili valori di 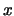 pesati con
pesati con 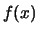 , dà il
baricentro della distribuzione; la deviazione standard, indicata
con
, dà il
baricentro della distribuzione; la deviazione standard, indicata
con 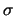 e calcolata come radice quadrata del momento di inerzia
della distribuzione
(leggi varianza: ``media dei quadrati degli scarti''),
fornisce la dispersione di valori che è possibile attendersi dalla
variabile.
e calcolata come radice quadrata del momento di inerzia
della distribuzione
(leggi varianza: ``media dei quadrati degli scarti''),
fornisce la dispersione di valori che è possibile attendersi dalla
variabile.
- Tutte le distribuzioni di variabile casuale sono subordinate ad
un certo stato di informazione. Utilizzando i due esempi precedenti
possiamo perciò scrivere
ove `` '' si legge ``dato'', ``subordinatamente a'', etc.
'' si legge ``dato'', ``subordinatamente a'', etc.
- L'intero stato di incertezza sui valori della grandezza di interesse
è espresso da
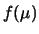 .
Da questa funzione è possibile calcolare la probabilità che
la grandezza abbia un valore compreso in un certo intervallo.
Per semplicità, spesso si riassume lo stato di informazione di
.
Da questa funzione è possibile calcolare la probabilità che
la grandezza abbia un valore compreso in un certo intervallo.
Per semplicità, spesso si riassume lo stato di informazione di
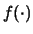 in due soli numeri:
E
in due soli numeri:
E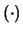 e
e 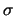 .
E' interessante l'interpretazione conoscitiva
di queste due grandezze. Esse possono essere viste come
la previsione e l'incertezza di previsione del numero
aleatorio.
.
E' interessante l'interpretazione conoscitiva
di queste due grandezze. Esse possono essere viste come
la previsione e l'incertezza di previsione del numero
aleatorio.
- Fra le distribuzioni di probabilità, quella più importante
per la trattazione delle incertezze di misura
è indubbiamente la ben nota gaussiana, che assumiamo nota.
Altre distribuzioni interessanti per le applicazioni sono la
distribuzione uniforme e la distribuzione triangolare.
Anche la distribuzione uniforme è
generalmente ben conosciuta. Ricordiamo soltanto che essa
ha una deviazione standard pari alla sua larghezza divisa
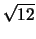 .
Utilizzando la semilarghezza
.
Utilizzando la semilarghezza 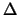 , si ha:
, si ha:
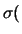
distr. uniforme
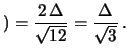
Essendo la distribuzione triangolare meno nota, essa
è descritta in Appendice C).
Nel caso ``isoscele'' (triangolare simmetrica)
di semiampiezza 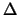 la deviazione standard vale
la deviazione standard vale
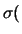
triangolare




Next: Valutazione dell'incertezza di misura:
Up: Errori e incertezze di
Previous: Probabilità soggettiva
Indice
Giulio D'Agostini
2001-04-02