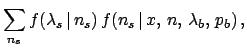Next: Conclusions
Up: Poisson background on the
Previous: Inferring
The histograms of
Fig. 11 show examples of the probability
distributions of 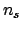 for
for 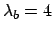 and three different
hypotheses for
and three different
hypotheses for 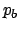 .
.
Figure:
Inference about 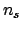 (histograms)
and
(histograms)
and  (continuous lines)
for
(continuous lines)
for 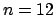 and
and 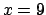 ,
assuming
,
assuming 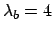 and three values of
and three values of
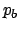 : 0.75, 0.25 and 0.95 (top down).
: 0.75, 0.25 and 0.95 (top down).
 |
These distributions quantify how much we believe that 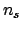 out of the observed
out of the observed 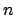 belong to the signal.
[By the way, the number
belong to the signal.
[By the way, the number 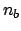 of background objects
present in the data can be inferred as complement
to
of background objects
present in the data can be inferred as complement
to 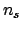 , since the two numbers are linearly dependent. It follows
that
, since the two numbers are linearly dependent. It follows
that
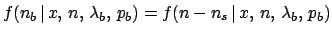 .]
.]
A different question is to infer the the Poisson  of the signal. Using once more Bayes theorem we get,
under the hypothesis of
of the signal. Using once more Bayes theorem we get,
under the hypothesis of 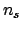 signal objects:
signal objects:
Assuming a uniform prior for  we get
(see e.g. Ref. [2]):
we get
(see e.g. Ref. [2]):
with expected value and variance both equal to
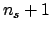 and mode equal to
and mode equal to 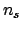 (the expected value is shifted
on the right side of the mode because the distribution is skewed
to the right).
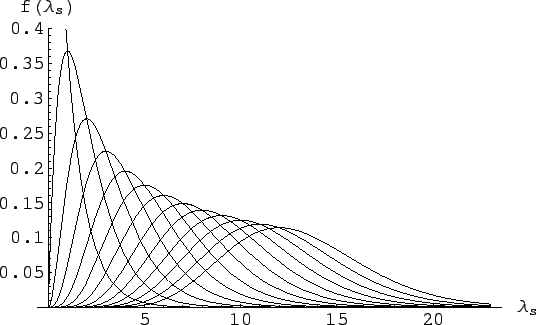
Figure 12
shows these pdf's, for
(the expected value is shifted
on the right side of the mode because the distribution is skewed
to the right).
Figure 12
shows these pdf's, for 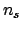 ranging from 0 to 12 and
assuming a uniform prior for
ranging from 0 to 12 and
assuming a uniform prior for  .
.
Figure:
Inference of  depending on the
depending on the 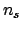 ,
ranging from 0 to 12 (left to right curves).
,
ranging from 0 to 12 (left to right curves).
 |
As far the pdf of  that depends on all possible
values of
that depends on all possible
values of 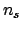 , each with is probability, is concerned,
we get from probability theory
[and remembering that, indeed,
, each with is probability, is concerned,
we get from probability theory
[and remembering that, indeed,
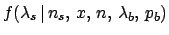 is equal to
is equal to
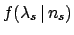 , because
, because 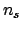 depends only on
depends only on
 , and then the other way around]:
, and then the other way around]:
i.e. the pdf of  is the weighted
average2
of the several
is the weighted
average2
of the several 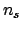 depending pdf's.
depending pdf's.
The results for the example we are considering in this
section are given in the plots of Fig. 11.



Next: Conclusions
Up: Poisson background on the
Previous: Inferring
Giulio D'Agostini
2004-12-13

![]() of the signal. Using once more Bayes theorem we get,
under the hypothesis of
of the signal. Using once more Bayes theorem we get,
under the hypothesis of ![]() signal objects:
signal objects:
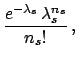
![]() that depends on all possible
values of
that depends on all possible
values of ![]() , each with is probability, is concerned,
we get from probability theory
[and remembering that, indeed,
, each with is probability, is concerned,
we get from probability theory
[and remembering that, indeed,
![]() is equal to
is equal to
![]() , because
, because ![]() depends only on
depends only on
![]() , and then the other way around]:
, and then the other way around]: